题目内容
如图，圆O是等腰三角形ABC的外接圆，AB＝AC，延长BC到点D，使CD＝AC，连结AD交圆O于点E，连结BE与AC交于点F.
(1)判断BE是否平分∠ABC，并说明理由；
(2)若AE＝6，BE＝8，求EF的长．
(1)判断BE是否平分∠ABC，并说明理由；
(2)若AE＝6，BE＝8，求EF的长．
（1）平分（2）
(1)BE平分∠ABC.
∵CD＝AC，∴∠D＝∠CAD.∵AB＝AC，∴∠ABC＝∠ACB.
∵∠EBC＝∠CAD，∴∠EBC＝∠D＝∠CAD.
∵∠ABC＝∠ABE＋∠EBC，∠ACB＝∠D＋∠CAD，
∴∠ABE＝∠EBC，即BE平分∠ABC.
(2)由(1)知∠CAD＝∠EBC＝∠ABE.∵∠AFE＝∠ABE，
∴△AEF∽△BEA.∴
.∵AE＝6，BE＝8，∴EF＝
.
∵CD＝AC，∴∠D＝∠CAD.∵AB＝AC，∴∠ABC＝∠ACB.
∵∠EBC＝∠CAD，∴∠EBC＝∠D＝∠CAD.
∵∠ABC＝∠ABE＋∠EBC，∠ACB＝∠D＋∠CAD，
∴∠ABE＝∠EBC，即BE平分∠ABC.
(2)由(1)知∠CAD＝∠EBC＝∠ABE.∵∠AFE＝∠ABE，
∴△AEF∽△BEA.∴
.∵AE＝6，BE＝8，∴EF＝.
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
是⊙
的直径，
是弧
的中点，
⊥
，
.
=
;
=4，⊙
的长.
，AF：FB：BE=4：2：1．若CE与圆相切，则CE的长为 ．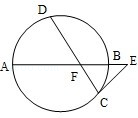
，OA＝
.
，
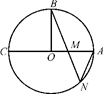
，则CP= ．