题目内容
如图,AB为⊙O的直径,C为⊙O上一点,AP和过C的切线互相垂直,垂足为P,过B的切线交过C的切线于T,PB交⊙O于Q,若∠BTC=120°,AB=4,则PQ·PB=( )


| A.2 | B.3 | C. | D.2 |
B
连接OC、AC,则OC⊥PC,
则O、C、T、B四点共圆,
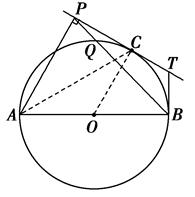
∵∠BTC=120°,∴∠COB=60°,
故∠AOC=120°.
由AO=OC=2知AC=2 ,
,
在Rt△APC中,
∠ACP=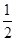 ∠AOC=60°,
∠AOC=60°,
因此PC= .根据切割线定理得PQ·PB=PC2=3.
.根据切割线定理得PQ·PB=PC2=3.
则O、C、T、B四点共圆,

∵∠BTC=120°,∴∠COB=60°,
故∠AOC=120°.
由AO=OC=2知AC=2
 ,
,在Rt△APC中,
∠ACP=
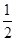 ∠AOC=60°,
∠AOC=60°,因此PC=
 .根据切割线定理得PQ·PB=PC2=3.
.根据切割线定理得PQ·PB=PC2=3.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的直径
的直径 的长为4,点
的长为4,点 平分弧
平分弧 ,过
,过 ,交
,交 .
.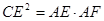 :
: 的角平分线,求
的角平分线,求 的长.
的长.
 是⊙
是⊙ 的直径,
的直径, 是弧
是弧 的中点,
的中点, ⊥
⊥ ,
, .
.
 =
= ;
; =4,⊙
=4,⊙ 的长.
的长. ,AF:FB:BE=4:2:1.若CE与圆相切,则CE的长为 .
,AF:FB:BE=4:2:1.若CE与圆相切,则CE的长为 .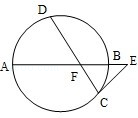
 的两条弦, AB与CD相交于点E,且
的两条弦, AB与CD相交于点E,且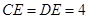 ,
,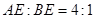 ,则
,则 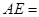 ______;
______;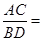 ______.
______.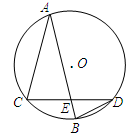


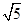 ,则AB=________.
,则AB=________.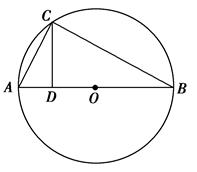
 ,
, ,则CP= .
,则CP= .