题目内容
15.若∠APB=∠BPC=∠CPA=60°,则直线PA与平面PBC所成角的余弦值为$\frac{\sqrt{3}}{3}$.分析 在PA上任选一点Q,过Q作QO⊥平面PBC于O点,连结PO,说明∠QPO即为PA与平面PBC所成的角,通过求解三角形的数据求解cos∠APO.
解答 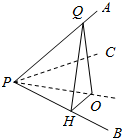 解:如图所示,在PA上任选一点Q
解:如图所示,在PA上任选一点Q
过Q作QO⊥平面PBC于O点,连结PO由于∠APB=∠APC=60°
∴PO为∠BPC的平分线,∠QPO即为PA与平面PBC所成的角
∠BPO=30°
作OH⊥PB于H,连QH
根据三垂线定理,QH⊥PH
RT△QPH中,∠QPH=60°,PQ=2PH
RT△OPH中,PO=$\frac{2\sqrt{3}}{3}PH$
RT△QPO中
cos∠APO=$\frac{PO}{QP}$=$\frac{\frac{2\sqrt{3}}{3}PH}{2PH}$=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查直线与平面所成角的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
5.已知点(3,-2)是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的点,则下列各点中,一定不在该椭圆上的是( )
| A. | (3,2) | B. | (-3,2) | C. | (-3,-2) | D. | (-2,3) |
6.在Rt△ABC中,CD是斜边上的高线,AC:BC=3:1,则S△ABC:S△BCD为( )
| A. | 4:3 | B. | 9:1 | C. | 10:1 | D. | 10:9 |
3.满足(n2-n-1)n+2=1的整数n有几个( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
10.某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
(1)假设n=2,求第一大块地都种植品种甲的概率;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如表:分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
| 品种甲 | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| 品种乙 | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如表:分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
4.双曲线x2-2y2=2的渐近线方程为( )
| A. | y=±$\frac{\sqrt{2}}{2}$x | B. | y=±$\sqrt{2}$x | C. | y=±$\frac{1}{2}$x | D. | y=±2x |