��Ŀ����
10��ijũ���ƻ���ֲij�������Ϊ�˶��������������Ʒ�֣��ֱ��ΪƷ�ּ�Ʒ���ң�����������飮ѡȡ�����أ�ÿ���طֳ�nС��أ����ܹ�2nС����У����ѡnС�����ֲƷ�ּף�����nС�����ֲƷ���ң�| Ʒ�ּ� | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| Ʒ���� | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
��2������ʱÿ���طֳ�8С�飬��n=8�����������õ�Ʒ�ּ�Ʒ�����ڸ�С����ϵ�ÿ�����������λ��kg/hm2��������ֱ���Ʒ�ּ�Ʒ���ҵ�ÿ�������������ƽ�����������������������������ΪӦ����ֲ��һƷ�֣�
���� ��1��������һ���ŵ���ͣ����鷢���������¼����ȴ�4С�������ѡ2С�����ֲƷ�ּĻ����¼���6���������������¼��ǵ�һ���ض���Ʒ�ּף����ݹŵ�����ʹ�ʽ�õ������
��2��������������Ʒ�ֵ�ÿ�������������ƽ�������������������Ʒ�ֵ�ƽ�����ͷ�����бȽϣ��õ��ҵ�ƽ�������ҵķ���Ƚ�С���õ������
��� �⣺��1�����һ�����е���С��ر��Ϊ1��2���ڶ������е���С��ر��Ϊ3��4��
���¼�A=����һ���ض���Ʒ�ּס���
��4С�������ѡ2С�����ֲƷ�ּĻ����¼���6����
��1��2������1��3������1��4������2��3������2��4������3��4����
���¼�A����1�������¼�����1��2����
����P��A��=$\frac{1}{6}$
��2��Ʒ�ּ�ÿ�������������ƽ��������������ֱ�Ϊ��
$\overline{{x}_{��}}$=$\frac{1}{8}$��403+397+390+404+388+400+412+406��=400��
S2��=$\frac{1}{8}$��32+��-3��2+��-10��2+42+��-12��2+02+122+62��=57.25��
Ʒ���ҵ�ÿ�������������ƽ��������������ֱ�Ϊ��
$\overline{x��}$=$\frac{1}{8}$��419+403+412+418+408+423+400+413��=412��
S2��=$\frac{1}{8}$��72+��-9��2+��0��2+62+��-4��2+112+��-12��2+12��=56��
�����Ͻ�����Կ�����Ʒ���ҵ�����ƽ��������Ʒ�ּ�����ƽ����������Ʒ�ֵ�����������첻��
��Ӧ��ѡ����ֲƷ���ң�
���� ���⿼��ŵ���͵ĸ��ʹ�ʽ�����������оٷ��õ��¼����������������ݵ�ƽ�����ͷ���Ĵ�С�Ƚϣ�����ƽ�����ͷ�������壬��һ���Ƚϼ��ۺ���Ŀ��

 ��У����ϵ�д�
��У����ϵ�д�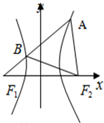 ��ͼ��F1��F2��˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1��a��0��b��0�������ҽ��㣬��F1��ֱ��l��˫���ߵ�������֧�ֱ��ڵ�A��B������ABF2Ϊ�ȱ������Σ���˫���ߵ�������Ϊ��������
��ͼ��F1��F2��˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1��a��0��b��0�������ҽ��㣬��F1��ֱ��l��˫���ߵ�������֧�ֱ��ڵ�A��B������ABF2Ϊ�ȱ������Σ���˫���ߵ�������Ϊ��������| A�� | 4 | B�� | $\sqrt{7}$ | C�� | $\frac{{2\sqrt{3}}}{3}$ | D�� | $\sqrt{3}$ |