题目内容
已知函数f(x)=px2+qx,其中p>0,p+q>1,对于数列{an},设它的前n项和为Sn,且满足Sn=f(n)(n∈N*).
(1)求数列{an}的通项公式,并证明an+1>an>1(n∈N*);
(2)求证:点M1(1,
),M2(2,
),M3(3,
),…,Mn(n,
)在同一直线l1上;
(3)若过点N1(1,a1),N2(2,a2)作直线l2,设l2与l1的夹角为θ,求tanθ的最大值.
(1)求数列{an}的通项公式,并证明an+1>an>1(n∈N*);
(2)求证:点M1(1,
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| Sn |
| n |
(3)若过点N1(1,a1),N2(2,a2)作直线l2,设l2与l1的夹角为θ,求tanθ的最大值.
(1)∵Sn=f(n)=pn2+qn∴当n=1时,a1=s1=p+q
当n≥2时,an=Sn-Sn-1=pn2+qn-[p(n-1)2+q(n-1)]=2pn-p+q
由于n=1时,a1=p+q适合上式,故数列{an}的通项公式为an=2pn-p+q…(3分)
又∵an+1-an=2p>0,
∴{an}是首项为p+q,公差为2p的等差数列,∴an+1>an>…>a1=p+q>1,
∴an+1>an>1…(4分)
(2)设Mi,Mj(i≠j)是M1,M2,…,Mn中任意两点,则Mi(i,
),Mj(j,
)
=P…(8分)
∴Mi,Mj两点连线的斜率为定值P,又Mi,Mj是M1,M2,…,Mn中任意两点,
∴点M1,M2,…,Mn在同一直线l1上…(9分)
(3)∵N1,N2两点连线的斜率为k2=
=2p,
又∵直线l1的斜率为k1=p,由夹角公式得
tanθ|
|=
=
≤
…(13分)
当且仅当
=2p即p=
时,上式等号成立.
故当p=
时,tanθ有最大值
…(14分)
当n≥2时,an=Sn-Sn-1=pn2+qn-[p(n-1)2+q(n-1)]=2pn-p+q
由于n=1时,a1=p+q适合上式,故数列{an}的通项公式为an=2pn-p+q…(3分)
又∵an+1-an=2p>0,
∴{an}是首项为p+q,公差为2p的等差数列,∴an+1>an>…>a1=p+q>1,
∴an+1>an>1…(4分)
(2)设Mi,Mj(i≠j)是M1,M2,…,Mn中任意两点,则Mi(i,
| Si |
| i |
| Sj |
| j |
|
=P…(8分)
∴Mi,Mj两点连线的斜率为定值P,又Mi,Mj是M1,M2,…,Mn中任意两点,
∴点M1,M2,…,Mn在同一直线l1上…(9分)
(3)∵N1,N2两点连线的斜率为k2=
| a2-a1 |
| 2-1 |
又∵直线l1的斜率为k1=p,由夹角公式得
tanθ|
| k1-k2 |
| 1+k1k2 |
| p |
| 1+2p2 |
| 1 | ||
|
| 1 | ||
2
|
当且仅当
| 1 |
| p |
| ||
| 2 |
故当p=
| ||
| 2 |
| ||
| 4 |

练习册系列答案
相关题目
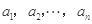 .对
.对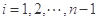 ,该数列前
,该数列前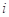 项的最大值记为
项的最大值记为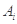 ,后
,后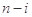 项
项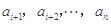 的最小值记为
的最小值记为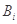 ,
,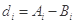 .
.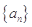 为3,4,7,1,写出
为3,4,7,1,写出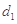 ,
,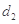 ,
,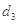 的值;
的值;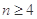 )是公比大于1的等比数列,且
)是公比大于1的等比数列,且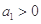 .证明:
.证明: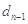 是等比数列.
是等比数列.