题目内容
已知数列{an}的前n项和Sn=n2-48n
（Ⅰ）求数列的通项公式an；
（Ⅱ）数列{an}是等差数列吗？如不是，请说明理由；如是，请给出证明，并求出该等差数列的首项与公差．
（Ⅰ）求数列的通项公式an；
（Ⅱ）数列{an}是等差数列吗？如不是，请说明理由；如是，请给出证明，并求出该等差数列的首项与公差．
（Ⅰ）当n≥2时，an=Sn-Sn-1=n2-48n-(n-1)2+48(n-1)=2n-49，
当n=1时，a1=S1=1-48=-47满足an，∴an=2n-49．
（Ⅱ）∵an=2n-49．
∴当n≥2时，an-an-1=2n-49-[2（n-1）-49]=2为常数，
∴数列{an}是等差数列，其中公差d=2，首项a1=S1=-47．
当n=1时，a1=S1=1-48=-47满足an，∴an=2n-49．
（Ⅱ）∵an=2n-49．
∴当n≥2时，an-an-1=2n-49-[2（n-1）-49]=2为常数，
∴数列{an}是等差数列，其中公差d=2，首项a1=S1=-47．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
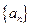的前
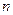项和为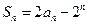
，
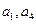（Ⅱ）证明：
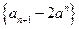是等比数列；（Ⅲ）求