题目内容
如图所示,在正方体ABCD-A1B1C1D1中,M、N分别是C1C、B1C1的中点.
求证:MN∥平面A1BD.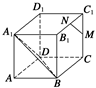
求证:MN∥平面A1BD.

证明略
方法一 如图所示,以D为原点,DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,

设正方体的棱长为1,则可求得
M(0,1,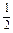 ),N(
),N(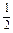 ,1,1),
,1,1),
D(0,0,0),A1(1,0,1),B(1,1,0),
于是 =(
=(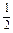 ,0,
,0,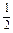 ),
),
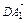 =(1,0,1),
=(1,0,1),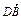 =(1,1,0).
=(1,1,0).
设平面A1BD的法向量是
n=(x,y,z).
则n·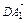 =0,且n·
=0,且n·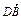 =0,
=0,
得
取x=1,得y=-1,z=-1.
∴n=(1,-1,-1).
又 ·n=(
·n=(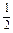 ,0,
,0,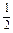 )·(1,-1,-1)=0,
)·(1,-1,-1)=0,
∴ ⊥n,
⊥n,
又∵
 平面A1BD,∴MN∥平面A1BD.
平面A1BD,∴MN∥平面A1BD.
方法二 ∵ =
= -
-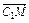 =
=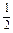
 -
-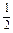

=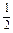 (
(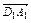 -
-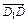 )=
)=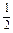
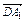 ,
,
∴ ∥
∥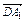 ,又∵MN
,又∵MN 平面A1BD.
平面A1BD.
∴MN∥平面A1BD.

设正方体的棱长为1,则可求得
M(0,1,
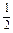 ),N(
),N(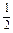 ,1,1),
,1,1),D(0,0,0),A1(1,0,1),B(1,1,0),
于是
 =(
=(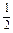 ,0,
,0,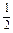 ),
),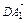 =(1,0,1),
=(1,0,1),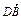 =(1,1,0).
=(1,1,0).设平面A1BD的法向量是
n=(x,y,z).
则n·
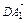 =0,且n·
=0,且n·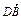 =0,
=0,得

取x=1,得y=-1,z=-1.
∴n=(1,-1,-1).
又
 ·n=(
·n=(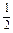 ,0,
,0,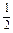 )·(1,-1,-1)=0,
)·(1,-1,-1)=0,∴
 ⊥n,
⊥n,又∵

 平面A1BD,∴MN∥平面A1BD.
平面A1BD,∴MN∥平面A1BD.方法二 ∵
 =
= -
-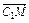 =
=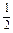
 -
-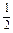

=
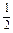 (
(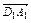 -
-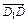 )=
)=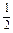
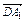 ,
,∴
 ∥
∥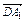 ,又∵MN
,又∵MN 平面A1BD.
平面A1BD.∴MN∥平面A1BD.

练习册系列答案
相关题目
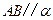 ,
,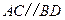 ,
,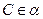 ,
,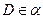 .求证
.求证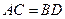 .
.
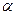 ,
,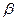 ,
,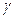 为三个平面,
为三个平面,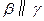 ,
,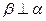 .求证:
.求证: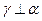 .
.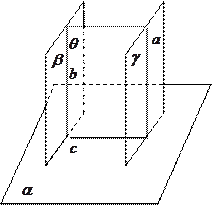
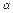 ∥平面
∥平面 ,点A∈
,点A∈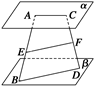 线段AB,CD上,且AE∶EB=CF∶FD.
线段AB,CD上,且AE∶EB=CF∶FD.