题目内容
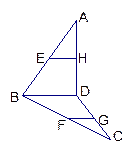
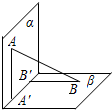
如图所示,平面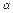 ∥平面
∥平面 ,点A∈
,点A∈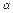 ,C∈
,C∈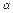 ,点B∈
,点B∈ ,D∈
,D∈ ,点E,F分别在
,点E,F分别在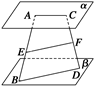 线段AB,CD上,且AE∶EB=CF∶FD.
线段AB,CD上,且AE∶EB=CF∶FD.
(1)求证:EF∥ ;
;
(2)若E,F分别是AB,CD的中点,AC=4,BD=6,且AC,BD所成的角为60°,
求EF的长.
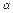 ∥平面
∥平面 ,点A∈
,点A∈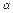 ,C∈
,C∈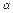 ,点B∈
,点B∈ ,D∈
,D∈ ,点E,F分别在
,点E,F分别在 线段AB,CD上,且AE∶EB=CF∶FD.
线段AB,CD上,且AE∶EB=CF∶FD.(1)求证:EF∥
 ;
;(2)若E,F分别是AB,CD的中点,AC=4,BD=6,且AC,BD所成的角为60°,
求EF的长.
(1)证明略(2)EF=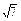 或EF=
或EF=
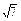 或EF=
或EF=
(1) ①当AB,CD在同一平面内时,

由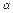 ∥
∥ ,平面
,平面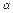 ∩平面ABDC=AC,
∩平面ABDC=AC,
平面 ∩平面ABDC=BD,∴AC∥BD, 2分
∩平面ABDC=BD,∴AC∥BD, 2分
∵AE∶EB=CF∶FD,∴EF∥BD,
又EF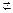
 ,BD
,BD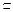
 ,∴EF∥
,∴EF∥ . 4分
. 4分
②当AB与CD异面时,
设平面ACD∩ =DH,且DH=AC.
=DH,且DH=AC.
∵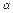 ∥
∥ ,
,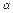 ∩平面ACDH=AC,
∩平面ACDH=AC,
∴AC∥DH,∴四边形ACDH是平行四边形, 6分
在AH上取一点G,使AG∶GH=CF∶FD,
又∵AE∶EB=CF∶FD,∴GF∥HD,EG∥BH,
又EG∩GF=G,∴平面EFG∥平面 .
.
∵EF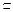 平面EFG,∴EF∥
平面EFG,∴EF∥ .综上,EF∥
.综上,EF∥ . 8分
. 8分
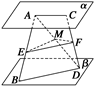
(2)解 如图所示,连接AD,取AD的中点M,连接ME,MF.
∵E,F分别为AB,CD的中点,
∴ME∥BD,MF∥AC,
且ME=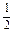 BD=3,MF=
BD=3,MF=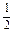 AC=2,
AC=2,
∴∠EMF为AC与BD所成的角(或其补角),
∴∠EMF=60°或120°, 12分
∴在△EFM中由余弦定理得,
EF=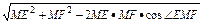
=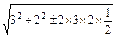 =
= ,
,
即EF=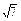 或EF=
或EF= . 16分
. 16分


由
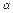 ∥
∥ ,平面
,平面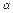 ∩平面ABDC=AC,
∩平面ABDC=AC,平面
 ∩平面ABDC=BD,∴AC∥BD, 2分
∩平面ABDC=BD,∴AC∥BD, 2分∵AE∶EB=CF∶FD,∴EF∥BD,
又EF
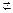
 ,BD
,BD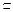
 ,∴EF∥
,∴EF∥ . 4分
. 4分②当AB与CD异面时,
设平面ACD∩
 =DH,且DH=AC.
=DH,且DH=AC.∵
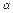 ∥
∥ ,
,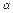 ∩平面ACDH=AC,
∩平面ACDH=AC,∴AC∥DH,∴四边形ACDH是平行四边形, 6分
在AH上取一点G,使AG∶GH=CF∶FD,
又∵AE∶EB=CF∶FD,∴GF∥HD,EG∥BH,
又EG∩GF=G,∴平面EFG∥平面
 .
.∵EF
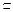 平面EFG,∴EF∥
平面EFG,∴EF∥ .综上,EF∥
.综上,EF∥ . 8分
. 8分(2)解 如图所示,连接AD,取AD的中点M,连接ME,MF.
∵E,F分别为AB,CD的中点,
∴ME∥BD,MF∥AC,
且ME=
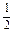 BD=3,MF=
BD=3,MF=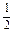 AC=2,
AC=2,∴∠EMF为AC与BD所成的角(或其补角),
∴∠EMF=60°或120°, 12分
∴在△EFM中由余弦定理得,
EF=
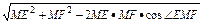
=
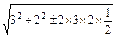 =
= ,
,即EF=
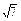 或EF=
或EF= . 16分
. 16分
练习册系列答案
相关题目
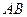 为异面直线
为异面直线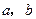 的公垂线,
的公垂线,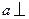 平面
平面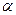 ,
,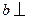 平面
平面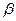 ,
,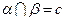 .求证:
.求证: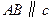 .
.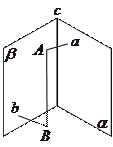
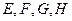 为空间四边形
为空间四边形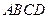 的边
的边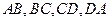 上的点,且
上的点,且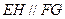 .求证:
.求证: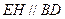 .
. 
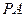 //平面
//平面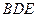 ;
;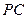 上是否存在点
上是否存在点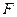 ,使三棱锥
,使三棱锥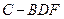 的
的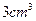 ?并说明理由.
?并说明理由.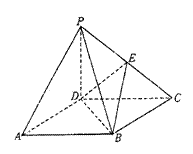

 a∥b;②a∥c,b∥c
a∥b;②a∥c,b∥c