题目内容
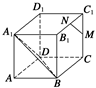
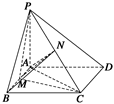
如图所示,正四棱锥P—ABCD的各棱长均为13,M,N分别为PA,BD上的点,且PM∶MA=BN∶ND=5∶8.
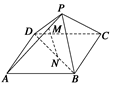
(1)求证:直线MN∥平面PBC;
(2)求线段MN的长.

(1)求证:直线MN∥平面PBC;
(2)求线段MN的长.
(1)证明略(2)7
(1)连接AN并延长交BC于Q,

连接PQ,如图所示.
∵AD∥BQ,∴△AND∽△QNB,
∴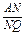 =
= =
=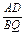 =
=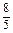 ,
,
又∵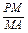 =
= =
=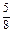 ,
,
∴ =
=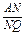 =
=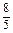 ,∴MN∥PQ,
,∴MN∥PQ,
又∵PQ 平面PBC,MN
平面PBC,MN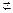 平面PBC,
平面PBC,
∴MN∥平面PBC.
(2)解 在等边△PBC中,∠PBC=60°,
在△PBQ中由余弦定理知
PQ2=PB2+BQ2-2PB·BQcos∠PBQ
=132+ -2×13×
-2×13×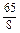 ×
× =
=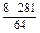 ,
,
∴PQ= ,
,
∵MN∥PQ,MN∶PQ=8∶13,
∴MN= ×
× =7.
=7.

连接PQ,如图所示.
∵AD∥BQ,∴△AND∽△QNB,
∴
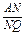 =
= =
=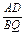 =
=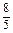 ,
,又∵
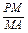 =
= =
=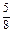 ,
,∴
 =
=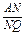 =
=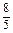 ,∴MN∥PQ,
,∴MN∥PQ,又∵PQ
 平面PBC,MN
平面PBC,MN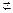 平面PBC,
平面PBC,∴MN∥平面PBC.
(2)解 在等边△PBC中,∠PBC=60°,
在△PBQ中由余弦定理知
PQ2=PB2+BQ2-2PB·BQcos∠PBQ
=132+
 -2×13×
-2×13×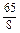 ×
× =
=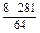 ,
,∴PQ=
 ,
,∵MN∥PQ,MN∶PQ=8∶13,
∴MN=
 ×
× =7.
=7.
练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 、
、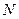 、
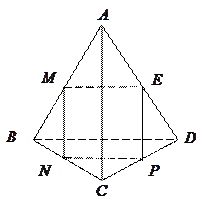
、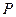 分别为空间四边形
分别为空间四边形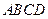 的边
的边 ,
,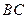 ,
,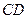 上的点,且
上的点,且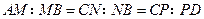 .
.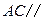 平面
平面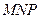 ,
, 平面
平面 的交线
的交线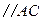 .
.
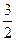
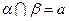 ,α⊥γ,β⊥γ,b∥α,b∥β.
,α⊥γ,β⊥γ,b∥α,b∥β.