题目内容
如图,已知椭圆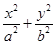 (a>b>0)的离心率
(a>b>0)的离心率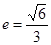 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.
(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由. 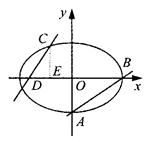
(1)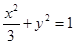 ;(2)
;(2)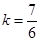 .
.
解析试题分析:(1)设椭圆的方程,用待定系数法求出 的值;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
的值;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式 :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论.
试题解析:解:(1)直线AB方程为:bx-ay-ab=0.
依题意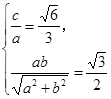 解得
解得 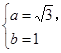
∴椭圆方程为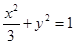 .[
.[
(2)假若存在这样的k值,由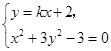 得
得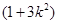
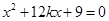 .
.
∴ 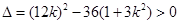 ①
①
设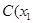 ,
,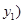 、
、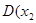 ,
,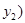 ,则
,则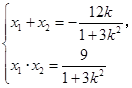 ②
②
而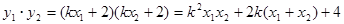 .
.
要使以CD为直径的圆过点E(-1,0),当且仅当CE⊥DE时,则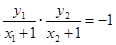 ,即
,即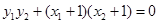 ∴
∴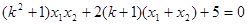 ③
③
将②式代入③整理解得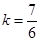 .经验证,
.经验证,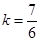 ,使①成立.
,使①成立.
综上可知,存在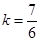 ,使得以CD为直径的圆过点E.
,使得以CD为直径的圆过点E.
考点:(1)椭圆的标准方程;(2)直线与椭圆的综合问题.

练习册系列答案
相关题目
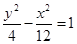 的焦点重合,它们的离心率之和为
的焦点重合,它们的离心率之和为 ,若椭圆的焦点在y轴上.
,若椭圆的焦点在y轴上. :
: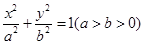 的左焦点
的左焦点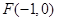 ,离心率为
,离心率为 ,函数
,函数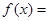
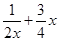 ,
, 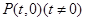 ,
,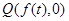 ,过
,过 的直线
的直线 交椭圆
交椭圆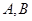 两点,求
两点,求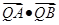 的最小值,并求此时的
的最小值,并求此时的 的值.
的值.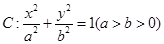 的离心率为
的离心率为 ,过顶点
,过顶点 的直线
的直线 与椭圆
与椭圆 .
. 在椭圆上且满足
在椭圆上且满足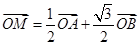 ,求直线
,求直线 的值.
的值. 分别是椭圆
分别是椭圆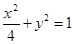 的左,右焦点.
的左,右焦点. 是椭圆在第一象限上一点,且
是椭圆在第一象限上一点,且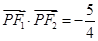 ,求
,求 的直线
的直线 与椭圆交于不同两点
与椭圆交于不同两点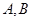 ,且
,且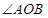 为锐角(其中
为锐角(其中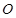 为原点),求直线
为原点),求直线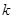 的取值范围.
的取值范围.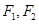 ,且
,且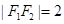 ,点
,点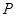 在椭圆上,且
在椭圆上,且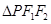 的周长为6.
的周长为6.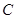 的方程;(2)若点
的方程;(2)若点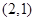 ,不过原点
,不过原点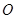 的直线
的直线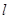 与椭圆
与椭圆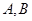 不同两点,设线段
不同两点,设线段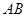 的中点为
的中点为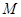 ,且
,且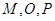 三点共线.设点
三点共线.设点 ,求
,求 )2+y2=4,(x-
)2+y2=4,(x-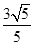 ,
,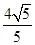 ),F(
),F(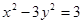 的离心率为
的离心率为 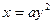 (a>0)的焦点,并且与x轴垂直,若l被抛物线截得的线段长为4,则a=
(a>0)的焦点,并且与x轴垂直,若l被抛物线截得的线段长为4,则a=