题目内容
已知椭圆 :
: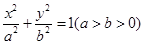 的左焦点
的左焦点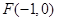 ,离心率为
,离心率为 ,函数
,函数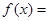
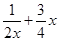 ,
,
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设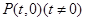 ,
,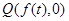 ,过
,过 的直线
的直线 交椭圆
交椭圆 于
于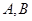 两点,求
两点,求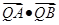 的最小值,并求此时的
的最小值,并求此时的 的值.
的值.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)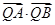 的最小值为
的最小值为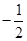 ,此时
,此时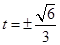 .
.
解析试题分析:(Ⅰ)利用左焦点F(-1,0),离心率为 ,及
,及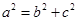 求出几何量,即可求椭圆C的标准方程;
求出几何量,即可求椭圆C的标准方程;
(Ⅱ)分类讨论,设直线l的方程来:y=k(x-t)代入抛物线方程,利用韦达定理,结合向量的数量积公式,即可求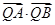 的最小值,并求此时的t的值.
的最小值,并求此时的t的值.
试题解析:(Ⅰ) ,由
,由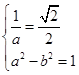 得
得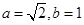 ,椭圆方程为
,椭圆方程为
(Ⅱ)若直线 斜率不存在,则
斜率不存在,则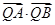 =
=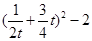
若直线 斜率存在,设直线
斜率存在,设直线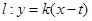 ,
,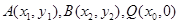
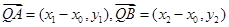
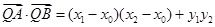
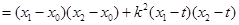
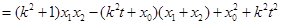
由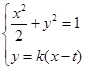 得
得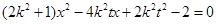
所以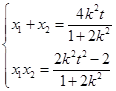
故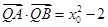
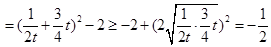
故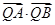 的最小值为
的最小值为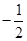 ,此时
,此时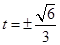 .
.
考点:直线与圆锥曲线的综合问题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
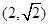
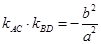 .
.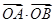 的最值:
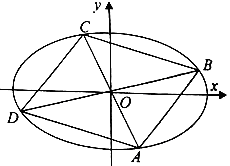
的最值: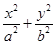 (a>b>0)的离心率
(a>b>0)的离心率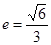 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
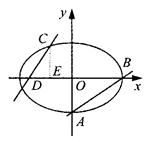
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.
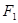 和
和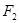 ,且|
,且|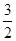 )在该椭圆上.
)在该椭圆上. 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若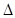 A
A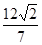 ,求以
,求以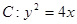 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.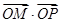 为定值;
为定值;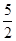 ,求向量
,求向量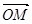 与
与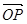 的夹角;
的夹角;
 相切于点P(2,1),且与
相切于点P(2,1),且与 轴交于点A,定点B的坐标为(2,0) .
轴交于点A,定点B的坐标为(2,0) .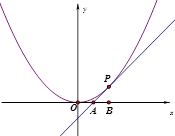
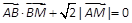 ,求点M的轨迹C;
,求点M的轨迹C;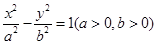 的一条渐近线方程是
的一条渐近线方程是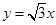 ,它的一个焦点与抛物线
,它的一个焦点与抛物线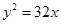 的焦点相同.则双曲线的方程为 .
的焦点相同.则双曲线的方程为 . 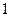 的直线
的直线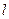 与椭圆
与椭圆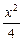 +y2=1相交于A、B两点,则|AB|的最大值为
+y2=1相交于A、B两点,则|AB|的最大值为
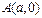 和
和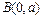 的直线与抛物线
的直线与抛物线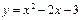 没有交点,那么实数
没有交点,那么实数 的取值范围是
的取值范围是