题目内容
设 分别是椭圆
分别是椭圆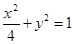 的左,右焦点.
的左,右焦点.
(1)若 是椭圆在第一象限上一点,且
是椭圆在第一象限上一点,且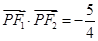 ,求
,求 点坐标;
点坐标;
(2)设过定点 的直线
的直线 与椭圆交于不同两点
与椭圆交于不同两点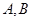 ,且
,且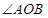 为锐角(其中
为锐角(其中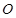 为原点),求直线
为原点),求直线 的斜率
的斜率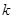 的取值范围.
的取值范围.
(1)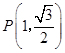 ;(2)
;(2)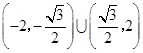 .
.
解析试题分析:(1)设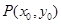 ,求
,求 点坐标,即要构建关于
点坐标,即要构建关于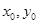 的两个方程,第一个方程可根据点在曲线上,点的坐标必须适合曲线的方程得到,即有
的两个方程,第一个方程可根据点在曲线上,点的坐标必须适合曲线的方程得到,即有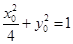 ,第二个方程可由
,第二个方程可由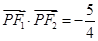 通过坐标化得到,即有
通过坐标化得到,即有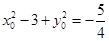 ,联立方程组,可解得
,联立方程组,可解得 点坐标;(2)求直线
点坐标;(2)求直线 的斜率
的斜率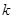 的取值范围,即要构建关于
的取值范围,即要构建关于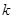 的不等式,可通过
的不等式,可通过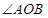 为锐角,转化为不等关系
为锐角,转化为不等关系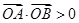 ,进而转化为关于
,进而转化为关于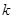 的不等式,解出
的不等式,解出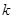 的取值范围.注意不要忽略
的取值范围.注意不要忽略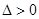 ,这是解析几何中常犯的错误.
,这是解析几何中常犯的错误.
试题解析:(1)依题意有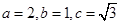 ,所以
,所以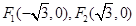 ,设
,设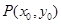 ,则由
,则由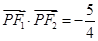 得:
得: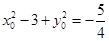 ,即
,即 ,又
,又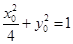 ,解得
,解得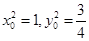 ,因为
,因为 是椭圆在第一象限上一点,所以
是椭圆在第一象限上一点,所以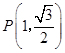 .
.
(2)设直线 与椭圆交于不同两点的坐标为
与椭圆交于不同两点的坐标为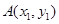 、
、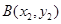 ,
,
将直线 :
: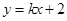 代入
代入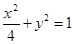 ,整理得:
,整理得: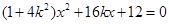 (
(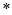 ),
),
则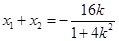 ,
,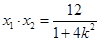 ,
,
因为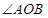 为锐角,所以
为锐角,所以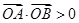 ,从而
,从而
整理得: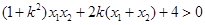 ,即
,即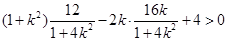 ,解得
,解得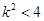 ,
,
且(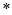 )方程必须满足:
)方程必须满足: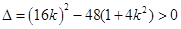 ,解得
,解得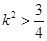 ,
,
因此有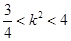 ,所以直线
,所以直线 的斜率
的斜率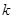 的取值范围为
的取值范围为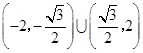 .
.
考点:1.直线与椭圆的位置关系;2.方程与不等式思想,3.设而不求的思想与等价转化思想.

练习册系列答案
相关题目
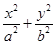 (a>b>0)的离心率
(a>b>0)的离心率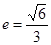 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
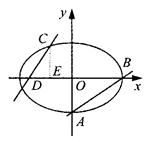
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.
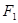 和
和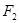 ,且|
,且|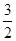 )在该椭圆上.
)在该椭圆上. 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若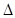 A
A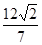 ,求以
,求以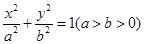 的离心率为
的离心率为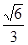 .
.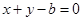 的距离为
的距离为 ,求椭圆的方程;
,求椭圆的方程;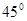 的直线和椭圆交于A,B两点.
的直线和椭圆交于A,B两点.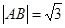 ,求b的值;
,求b的值;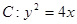 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.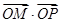 为定值;
为定值;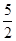 ,求向量
,求向量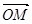 与
与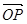 的夹角;
的夹角;
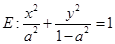 的焦点在
的焦点在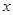 轴上.
轴上.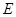 的焦距为1,求椭圆
的焦距为1,求椭圆 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点, 为椭圆
为椭圆 交
交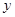 轴与点
轴与点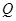 ,并且
,并且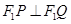 ,证明:当
,证明:当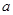 变化时,点
变化时,点 在某定直线上.
在某定直线上. 的焦点
的焦点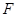 的直线交抛物线于
的直线交抛物线于 ,
, 两点.求证:
两点.求证: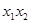 为定值;
为定值;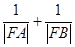 为定值.
为定值.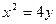 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆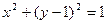 于点A、B、C、D,则
于点A、B、C、D,则 的值是_____
的值是_____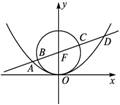
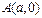 和
和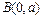 的直线与抛物线
的直线与抛物线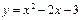 没有交点,那么实数
没有交点,那么实数 的取值范围是
的取值范围是