题目内容
已知椭圆的顶点与双曲线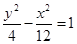 的焦点重合,它们的离心率之和为
的焦点重合,它们的离心率之和为 ,若椭圆的焦点在y轴上.
,若椭圆的焦点在y轴上.
(1)求双曲线的离心率,并写出其渐近线方程;
(2)求椭圆的标准方程.
(1)e1=2,渐近线方程为y=±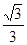 ;(2)
;(2)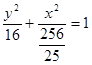 .
.
解析试题分析:(1)首先由已知双曲线的标准方程求出双曲线的几何量,就可得焦点及离心率,渐近线方程;
(2)根据已知条件求出椭圆的离心率及焦距,利用椭圆的三个参数的关系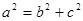 ,求出椭圆中的三个参数,从而就可求出椭圆的方程.
,求出椭圆中的三个参数,从而就可求出椭圆的方程.
试题解析:(1)设双曲线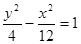 的焦距为2c1,离心率为e1,(2分)
的焦距为2c1,离心率为e1,(2分)
则有:c12=4+12=16,c1=4 (4分)
∴e1=2,渐近线方程为y=±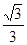 ;(6分)
;(6分)
(2)椭圆的离心率为 ,∴
,∴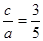 .又a=4,∴c=
.又a=4,∴c= ;
;
∵a2=b2+c2,(10分)
∴b2=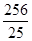 ;∴所求椭圆方程为
;∴所求椭圆方程为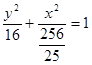 (12分)
(12分)
考点:1.双曲线的简单性质;2.椭圆的标准方程.

练习册系列答案
相关题目
 经过点
经过点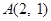 ,离心率为
,离心率为 ,过点
,过点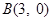 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 .
.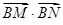 的取值范围.
的取值范围.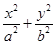 (a>b>0)的离心率
(a>b>0)的离心率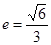 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
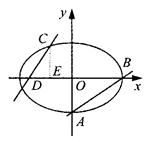
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.
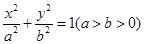 的离心率为
的离心率为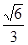 .
.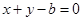 的距离为
的距离为 ,求椭圆的方程;
,求椭圆的方程;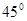 的直线和椭圆交于A,B两点.
的直线和椭圆交于A,B两点.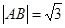 ,求b的值;
,求b的值;
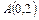 及椭圆
及椭圆 上任意一点
上任意一点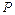 ,则
,则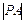 最大值为 。
最大值为 。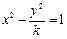 的焦点到渐近线的距离为
的焦点到渐近线的距离为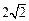 ,则实数k的值是
,则实数k的值是 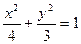 的左准为准线的抛物线交椭圆C的右准
的左准为准线的抛物线交椭圆C的右准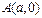 和
和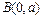 的直线与抛物线
的直线与抛物线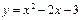 没有交点,那么实数
没有交点,那么实数 的取值范围是
的取值范围是