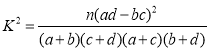题目内容
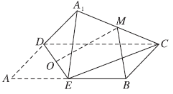
【题目】已知四面体![]() 中,棱
中,棱![]() ,
,![]() 所在直线所成角为
所在直线所成角为![]() ,且
,且![]() ,
,![]() ,
,![]() ,面
,面![]() 和面
和面![]() 所成的锐二面角为
所成的锐二面角为![]() ,面
,面![]() 和面
和面![]() 所成的锐二面角为
所成的锐二面角为![]() ,当四面体
,当四面体![]() 的体积取得最大值时( ).
的体积取得最大值时( ).
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
【答案】A
【解析】
利用余弦定理及基本不等式,求出![]() ,进而得到当
,进而得到当![]() 为等边三角形时,
为等边三角形时,![]() 的面积取到最大值,再根据面面垂直的性质定理及二面角的定义,即可得到结果.
的面积取到最大值,再根据面面垂直的性质定理及二面角的定义,即可得到结果.
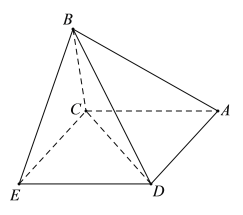
![]() ,即
,即![]() ,
,
整理得![]() ,
,
解得![]() ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
所以,![]() ,
,
所以,当![]() 为等边三角形时,
为等边三角形时,![]() 的面积取到最大值.
的面积取到最大值.
过![]() 作
作![]() ∥
∥![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,
,
则四边形![]() 为菱形,
为菱形,
因为![]() ,
,![]() 所在直线所成角为
所在直线所成角为![]() ,所以
,所以![]() ,
,
当面![]() 面
面![]() 时,四面体
时,四面体![]() 的高取得最大值,
的高取得最大值,
![]() ,即
,即![]() ,解得
,解得![]() ,
,
因为![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() ,
,
又因为面![]() 面
面![]() ,所以
,所以![]() 面
面![]() ,
,
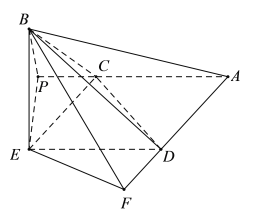
过![]() 作
作![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
连接![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以![]() 为面
为面![]() 和面
和面![]() 所成的二面角,
所成的二面角,
![]() 为面
为面![]() 和面
和面![]() 所成的锐二面角,
所成的锐二面角,
即![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() .
.
故选:A.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】2020年新型冠状病毒肺炎(简称“新冠肺炎”)成为威胁全球的公共卫生问题,中医药在本次新冠肺炎的治疗中发挥了重要作用.研究人员对66例普通型新冠肺炎恢复期患者进行了中医临床特征分析,发现主要证型有气阴两虚证与肺脾气虚证,同时可能兼夹湿证.为研究这两种主要证型在兼夹湿证的难易上是否有差异,研究人员将湿证症状分级量化,将所有肺脾气虚证患者的量化分作成茎叶图.
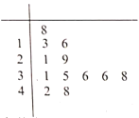
(1)若量化分不低于16分,即可诊断为兼夹湿证,请参考茎叶图,完成下面![]() 列联表.
列联表.
夹湿证 | 非夹湿证 | 合计 | |
气阴两虚 | 20 | ||
肺脾气虚 | |||
合计 | 66 |
(2)根据此资料,能否有99%的把握认为两种主要证型在兼夹湿证的难易上有差异?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |