题目内容
【题目】函数f(x)=ex+asinx,x∈(-π,+∞),下列说法正确的是( )
A.当a=1时,f(x)在(0,f(0))处的切线方程为2x-y+1=0
B.当a=1时,f(x)存在唯一极小值点x0且-1<f(x0)<0
C.对任意a>0,f(x)在(-π,+∞)上均存在零点
D.存在a<0,f(x)在(-π,+∞)上有且只有一个零点
【答案】ABD
【解析】
逐一验证选项,选项A,通过切点求切线,再通过点斜式写出切线方程,选项B 通过导数求出函数极值并判断极值范围,选项C、D,通过构造函数,将零点问题转化判断函数与直线y=a 的交点问题.
选项A,当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() ,故切点为
,故切点为![]() ,
,![]() ,
,
所以切线斜率![]() ,
,
故直线方程为:![]() ,即切线方程为:
,即切线方程为:![]() , 选项A正确.
, 选项A正确.
选项B,当![]() 时,
时,![]() ,
,![]() ,
,![]()
![]() 恒成立,所以
恒成立,所以![]() 单调递增,
单调递增,
又![]() ,
,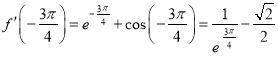
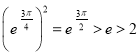 ,所以
,所以![]() ,即
,即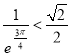 ,所以
,所以![]()
所以存在![]() ,使得
,使得![]() ,即
,即![]()
则在![]() 上,
上,![]() ,在
,在![]() 上,
上,![]() ,
,
所以在![]() 上,
上,![]() 单调递减,在
单调递减,在![]() 上,
上,![]() 单调递增.
单调递增.
所以![]() 存在唯一的极小值点
存在唯一的极小值点![]() .
.
![]()
![]() ,则
,则![]() ,
,![]() ,所以B正确.
,所以B正确.
对于选项C、D,![]() ,
,![]()
令![]() ,即
,即 ![]() ,所以
,所以![]() , 则令
, 则令![]() ,
,![]()
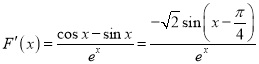 ,令
,令![]() ,得
,得![]()
由函数![]() 的图像性质可知:
的图像性质可知:
![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以![]() 时,
时,![]() 取得极小值,
取得极小值,
即当![]() 时
时![]() 取得极小值,
取得极小值,
又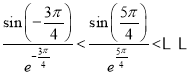 ,即
,即![]()
又因为在![]() 上
上![]() 单调递减,所以
单调递减,所以![]()
所以![]() 时,
时,![]() 取得极小值,
取得极小值,
即当![]() 时
时![]() 取得极大值,
取得极大值,
又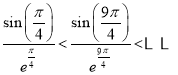 ,即
,即![]()
所以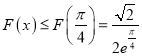
当![]() 时,
时,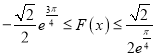
所以当![]() ,即
,即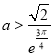 时,f(x)在(-π,+∞)上无零点,所以C不正确.
时,f(x)在(-π,+∞)上无零点,所以C不正确.
当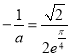 ,即
,即![]() 时,
时,![]() 与
与![]() 的图象只有一个交点
的图象只有一个交点
即存在a<0,f(x)在(-π,+∞)上有且只有一个零点,故D正确.
故选:ABD
.

【题目】在创建“全国文明卫生城”过程中,某市“创城办”为了调查市民对创城工作的了解情况,进行了一次创城知识问卷调查(一位市民只能参加一次).通过随机抽样,得到参加问卷调查的100人的得分统计结果如表所示:
组别 | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 2 | 15 | 20 | 25 | 24 | 10 | 4 |
(I)由频数分布表可以大致认为,此次问卷调查的得分Z服从正态分布N(μ,198),μ近似为这100人得分的平均值(同一组中的数据用该组区间的中点值作代表),利用该正态分布,求P(37<Z≤79);
(II)在(I)的条件下,“创城办”为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于μ的可以获赠2次随机话费,得分低于μ的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
赠送话费的金额(单元:元) | 20 | 40 |
概率 |
|
|
现有市民甲参加此次问卷调查,记ξ(单位:元)为该市民参加问卷调查获赠的话费,求ξ的分布列与数学期望.附:参考数据与公式:![]() 14.
14.
若X~N(μ,σ2),则P(μ﹣σ<X≤μ+σ)=0.6826;P(μ2σ<X≤μ+2σ)=0.9544,P(μ﹣3σ<X≤μ+3σ)=0.9974.
