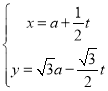题目内容
【题目】已知动圆P经过点![]() ,并且与圆
,并且与圆![]() 相切.
相切.
(Ⅰ)求圆心P的轨迹C的方程;
(Ⅱ)O是坐标原点,过点![]() 的直线
的直线![]() 与C交于A,B两点,在C上是否存在点Q,使得四边形
与C交于A,B两点,在C上是否存在点Q,使得四边形![]() 是平行四边形?
是平行四边形?
【答案】(1) ![]() ;
;
(2) 直线![]() 为
为![]() 或
或![]() 时,椭圆C上存在点Q,否则不存在.
时,椭圆C上存在点Q,否则不存在.
【解析】
(1) 由椭圆的定义可得,P的轨迹是以M,N为焦点的椭圆,进而求出方程.
(2) 假设存在,根据平行四边形已知三个点坐标,表示Q的坐标,设直线方程,联立直线和椭圆方程,利用韦达定理整理Q的坐标,根据Q在椭圆上,求得直线方程.
(1) 由题意可得N在圆M内部,所以两圆内切,
所以![]() ,
,
由椭圆的定义可知,点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点的椭圆,
为焦点的椭圆,
设椭圆方程为![]() ,
,
其中![]() ,
,![]() ,
,
所以![]() ,
,
所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2) 假设C上存在点Q,使得四边形![]() 是平行四边形,
是平行四边形,
由题意可知,直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为:
的方程为:![]()
设直线![]() 与椭圆C的交点
与椭圆C的交点![]() ,
,
则![]()
联立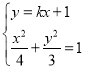 可得,
可得,![]()
由韦达定理可得,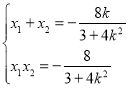
![]()
所以![]() ,
,
点 Q在椭圆C上,所以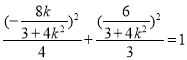 ,
,
解得![]()
综上可得,直线![]() 为
为![]() 或
或![]() 时,
时,
椭圆C上存在点Q,使得四边形![]() 是平行四边形,否则不存在.
是平行四边形,否则不存在.

【题目】某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度![]() (每层玻璃的厚度相同)及两层玻璃间夹空气层厚度
(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度![]() 对保温效果的影响,利用热传导定律得到热传导量
对保温效果的影响,利用热传导定律得到热传导量![]() 满足关系式
满足关系式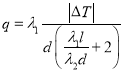 ,其中玻璃的热传导系数
,其中玻璃的热传导系数![]() 焦耳/(厘米·度),不流通、干燥空气的热传导系数
焦耳/(厘米·度),不流通、干燥空气的热传导系数![]() 焦耳/(厘米·度),
焦耳/(厘米·度),![]() 为室内外温度差,
为室内外温度差,![]() 值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
型号 | 每层玻璃厚度 | 玻璃间夹空气层厚度 |
| 0.4 | 3 |
| 0.3 | 4 |
| 0.5 | 3 |
| 0.4 | 4 |
则保温效果最好的双层玻璃的型号是( )
A.![]() 型B.
型B.![]() 型C.
型C.![]() 型D.
型D.![]() 型
型
【题目】从![]() 年底开始,非洲东部的肯尼亚等国家爆发出了一场严重的蝗虫灾情.目前,蝗虫已抵达乌干达和坦桑尼亚,并向西亚和南亚等地区蔓延.蝗虫危害大,主要危害禾本科植物,能对农作物造成严重伤害,每只蝗虫的平均产卵数
年底开始,非洲东部的肯尼亚等国家爆发出了一场严重的蝗虫灾情.目前,蝗虫已抵达乌干达和坦桑尼亚,并向西亚和南亚等地区蔓延.蝗虫危害大,主要危害禾本科植物,能对农作物造成严重伤害,每只蝗虫的平均产卵数![]() 和平均温度
和平均温度![]() 有关,现收集了以往某地的
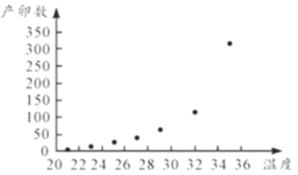
有关,现收集了以往某地的![]() 组数据,得到下面的散点图及一些统计量的值.
组数据,得到下面的散点图及一些统计量的值.
平均温度 |
|
|
|
|
|
|
|
平均产卵数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() (其中
(其中![]() 为自然对数的底数)哪一个更适宜作为平均产卵数
为自然对数的底数)哪一个更适宜作为平均产卵数![]() 关于平均温度
关于平均温度![]() 的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出
的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出![]() 关于
关于![]() 的回归方程.(结果精确到小数点后第三位)
的回归方程.(结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到![]() 以上时蝗虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治,记该地每年平均温度达到
以上时蝗虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治,记该地每年平均温度达到![]() 以上的概率为
以上的概率为![]() .
.
①记该地今后![]() 年中,恰好需要
年中,恰好需要![]() 次人工防治的概率为
次人工防治的概率为![]() ,求
,求![]() 取得最大值时相应的概率
取得最大值时相应的概率![]() ;
;
②根据①中的结论,当![]() 取最大值时,记该地今后
取最大值时,记该地今后![]() 年中,需要人工防治的次数为
年中,需要人工防治的次数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
附:对于一组数据![]() 、
、![]() 、
、![]() 、
、![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: ,
,![]() .
.