题目内容
已知: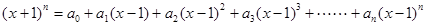
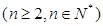
(1)当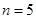 时,求
时,求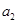 的值。
的值。
(2)设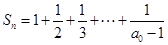 ,求证:
,求证: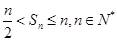 。
。
(1)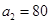 (2)利用不等式的放缩法来得到证明。
(2)利用不等式的放缩法来得到证明。
解析试题分析:(1)根据题意,由于(1)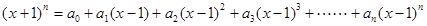 ,那么当
,那么当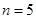 时,
时, 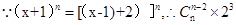 表示的为
表示的为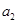 的值,且为80.
的值,且为80.
故可知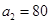
(2)由于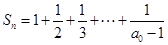 ,令x=1,则可知
,令x=1,则可知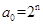 ,那么可知当n=1时,可以知道不等式左边为
,那么可知当n=1时,可以知道不等式左边为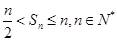
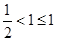 成立,假设当n=k,时,
成立,假设当n=k,时,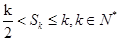 ,
,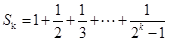 那么当n=k+1时,则可知
那么当n=k+1时,则可知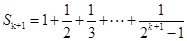 ,则可知
,则可知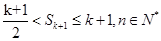 即可,那么结合假设推理论证并分析可知成立。
即可,那么结合假设推理论证并分析可知成立。
考点:不等式的证明,以及二项式定理
点评:主要是考查了二项式定理以及不等式证明的运用,属于难度题。

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 ,
,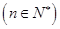 .
.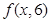 的展开式中系数最大的项;
的展开式中系数最大的项;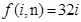 (
(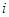 为虚数单位),求
为虚数单位),求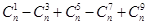 .
.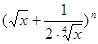 的展开式前三项中的
的展开式前三项中的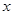 的系数成等差数列.
的系数成等差数列.