题目内容
已知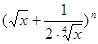 的展开式前三项中的
的展开式前三项中的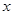 的系数成等差数列.
的系数成等差数列.
(1)展开式中所有的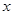 的有理项为第几项?
的有理项为第几项?
(2)求展开式中系数最大的项.
(1)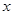 的有理项为第1,5,9项。(2)所求项分别为
的有理项为第1,5,9项。(2)所求项分别为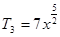 和
和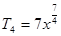 .
.
解析试题分析:(1)展开式前三项的系数分别为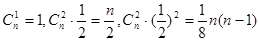 .
.
由题设可知: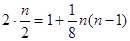 ,解得:n=8或n=1(舍去).
,解得:n=8或n=1(舍去).
当n=8时,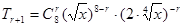 =
=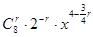 .
.
据题意,4-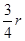 必为整数,从而可知
必为整数,从而可知 必为4的倍数,
必为4的倍数,
而0≤ ≤8,∴
≤8,∴ =0,4,8.
=0,4,8.
故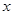 的有理项为第1,5,9项。
的有理项为第1,5,9项。
(2)设第 +1项的系数
+1项的系数 最大,显然
最大,显然 >0,
>0,
故有 ≥1且
≥1且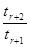 ≤1.
≤1.
∵ =
=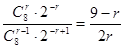 ,由
,由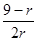 ≥1,得
≥1,得 ≤3.
≤3.
∵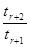 =
=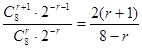 ,由
,由 ≤1,得
≤1,得 ≥2.
≥2.
∴ =2或
=2或 =3,所求项分别为
=3,所求项分别为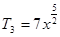 和
和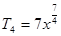 .
.
考点:二项展开式的通项公式,等差数列的概念,简单不等式解法。
点评:中档题,本题主要考查二项展开式的通项公式,等差数列的概念,简单不等式解法。解答思路比较明确,对计算能力要求较高。

练习册系列答案
相关题目
 的展开式中前三项的系数成等差数列.设
的展开式中前三项的系数成等差数列.设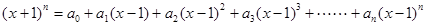
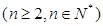
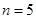 时,求
时,求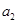 的值。
的值。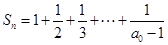 ,求证:
,求证: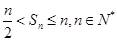 。
。 的展开式中偶数项二项式系数和比
的展开式中偶数项二项式系数和比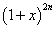 展开式中奇数项二项式系数和小
展开式中奇数项二项式系数和小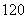 ,求:
,求: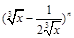 的展开式中,第6项
的展开式中,第6项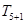 为常数项.
为常数项.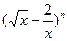 展开式中第三项的系数比第二项的系数大162,求:
展开式中第三项的系数比第二项的系数大162,求: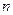 的值;
的值;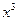 的项.
的项.