题目内容
4个男同学,3个女同学站成一排.
(1)男生甲必须排在正中间,有多少种不同的排法?
(2)3个女同学必须排在一起,有多少种不同的排法?
(3)任何两个女同学彼此不相邻,有多少种不同的排法?
(4)其中甲、乙两名同学之间必须有3人,有多少种不同的排法?
(用数字作答)
(1)720,(2)720,(3)1440,(4)720
解析试题分析:(1) ; 3分
; 3分
(2)(捆绑法)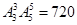 7分
7分
(3)(插空法)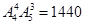 ; 11分
; 11分
(4)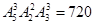 . 15分
. 15分
考点:本题考查了排列的实际运用
点评:关于排列组合应用题,从排列的角度来讲,它主要有三种题型:“在”与“不在”,“邻”与“不邻”,定序排列。“在”与“不在”中,要先考虑条件元素,即先考虑固定元素或特殊元素,若从位置角度分析,先考虑固定位置或特殊位置。“邻”是集组排列,即采用捆绑法,“不邻”是插空排列,而定序排列有固定公式:一般地,若n个元素排队,其中有m个元素顺序一定,这m个元素不一定相邻,则不同排法 。组合中常见题型有“至少”、“至多”问题,“含与不含”问题。在“至少”、“至多”问题中,可直接法来解,须分类,应做到不重不漏;也可间接法来解,即整体排除法,利用这种方法时,应把握好“至多”或“至少”的对立面。“含与不含”是选的范畴问题,同时也可利用它来理解组合数的性质。含或不含某元素,在选时不必再考虑,如在n个不同元素中选m个元素(n<m),若甲必选的选法有
。组合中常见题型有“至少”、“至多”问题,“含与不含”问题。在“至少”、“至多”问题中,可直接法来解,须分类,应做到不重不漏;也可间接法来解,即整体排除法,利用这种方法时,应把握好“至多”或“至少”的对立面。“含与不含”是选的范畴问题,同时也可利用它来理解组合数的性质。含或不含某元素,在选时不必再考虑,如在n个不同元素中选m个元素(n<m),若甲必选的选法有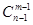 ,若甲不选,则选法有
,若甲不选,则选法有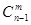

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
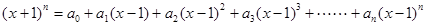
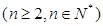
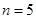 时,求
时,求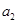 的值。
的值。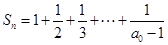 ,求证:
,求证: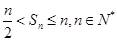 。
。 的展开式中偶数项二项式系数和比
的展开式中偶数项二项式系数和比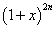 展开式中奇数项二项式系数和小
展开式中奇数项二项式系数和小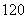 ,求:
,求: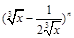 的展开式中,第6项
的展开式中,第6项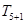 为常数项.
为常数项.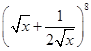 的展开式中,求
的展开式中,求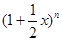 展开式的各项依次记为
展开式的各项依次记为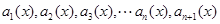 .
.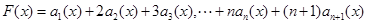 .
.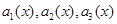 的系数依次成等差数列,求
的系数依次成等差数列,求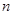 的值;
的值;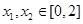 ,恒有
,恒有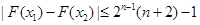 .
.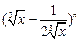 的展开式中,前三项系数的绝对值成等差数列.
的展开式中,前三项系数的绝对值成等差数列. 的值;
的值; II)求展开式的常数项.
II)求展开式的常数项.