Question

【题目】为了解学生的课外阅读时间情况，某学校随机抽取了50人进行统计分析，把这50人每天阅读的时间（单位：分钟）绘制成频数分布表，如下表所示：

阅读时间
人数	8	10	12	11	7	2

若把每天阅读时间在60分钟以上（含60分钟）的同学称为“阅读达人”，根据统计结果中男女生阅读达人的数据，制作成如图所示的等高条形图.

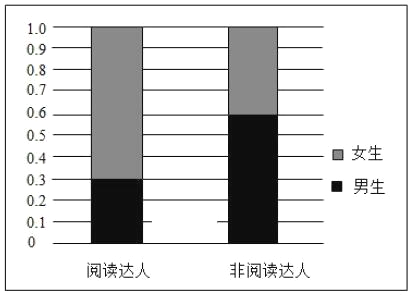
（1）根据抽样结果估计该校学生的每天平均阅读时间（同一组数据用该区间的终点值作为代表）；

（2）根据已知条件完成下面的列联表，并判断是否有99%的把握认为“阅读达人”跟性别有关？

	男生	女生	总计
阅读达人
非阅读达人
总计

附：参考公式，其中.

临界值表：

（）	0.100	0.050	0.010	0.001
	2.706	3.841	6.635	10.828

Answer 1

【答案】(1)52（分）.

(2)列联表见解析；没有99%的把握认为“阅读达人跟性别有关.

【解析】分析：（1）由可求出该学生的每天平均阅读时间；（2）由频数分布表结合等高条形图作出列联表，利用公式计算观测值，对照临界值即可得出结论.

详解：（1）该校学生的每天平均阅读时间为：

（分）；

（2）由频数分布表得，“阅读达人”的人数是人，

根据等高条形图作出列联表如下：

	男生	女生	总计
阅读达人	6	14	20
非阅读达人	18	12	30
总计	24	26	50

计算，

由于，故没有99%的把握认为“阅读达人跟性别有关.