题目内容
【题目】设实数c>0,整数p>1,n∈N* .
(1)证明:当x>﹣1且x≠0时,(1+x)p>1+px;
(2)数列{an}满足a1> ![]() ,an+1=
,an+1= ![]() an+
an+ ![]() an1﹣p . 证明:an>an+1>
an1﹣p . 证明:an>an+1> ![]() .
.
【答案】
(1)
证明:令f(x)=(1+x)p﹣(1+px),则f′(x)=p(1+x)p﹣1﹣p=p[(1+x)p﹣1﹣1].
①当﹣1<x<0时,0<1+x<1,由p>1知p﹣1>0,∴(1+x)p﹣1<(1+x)0=1,
∴(1+x)p﹣1﹣1<0,即f′(x)<0,
∴f(x)在(﹣1,0]上为减函数,
∴f(x)>f(0)=(1+0)p﹣(1+p×0)=0,即(1+x)p﹣(1+px)>0,
∴(1+x)p>1+px.
②当x>0时,有1+x>1,得(1+x)p﹣1>(1+x)0=1,
∴f′(x)>0,
∴f(x)在[0,+∞)上为增函数,
∴f(x)>f(0)=0,
∴(1+x)p>1+px.
综合①、②知,当x>﹣1且x≠0时,都有(1+x)p>1+px,得证.
(2)
证明:先证an+1> ![]() .
.
∵an+1= ![]() an+
an+ ![]() an1﹣p,∴只需证
an1﹣p,∴只需证 ![]() an+
an+ ![]() an1﹣p>
an1﹣p> ![]() ,
,
将 ![]() 写成p﹣1个
写成p﹣1个 ![]() 相加,上式左边=
相加,上式左边= ![]()
![]() ,
,
当且仅当 ![]() ,即
,即 ![]() 时,上式取“=”号,
时,上式取“=”号,
当n=1时,由题设知 ![]() ,∴上式“=”号不成立,
,∴上式“=”号不成立,
∴ ![]() an+
an+ ![]() an1﹣p>
an1﹣p> ![]() ,即an+1>
,即an+1> ![]() .
.
再证an>an+1.
只需证an> ![]() an+
an+ ![]() an1﹣p,化简、整理得anp>c,只需证an>
an1﹣p,化简、整理得anp>c,只需证an> ![]() .
.
由前知an+1> ![]() 成立,即从数列{an}的第2项开始成立,
成立,即从数列{an}的第2项开始成立,
又n=1时,由题设知 ![]() 成立,
成立,
∴ ![]() 对n∈N*成立,∴an>an+1.
对n∈N*成立,∴an>an+1.
综上知,an>an+1> ![]() ,原不等式得证.
,原不等式得证.
【解析】第(1)问中,可构造函数f(x)=(1+x)p﹣(1+px),求导数后利用函数的单调性求解;
对第(2)问,从an+1 ![]() 着手,由an+1=
着手,由an+1= ![]() an+
an+ ![]() an1﹣p , 将求证式进行等价转化后即可解决,用相同的方式将an>an+1进行转换,设法利用已证结论证明.
an1﹣p , 将求证式进行等价转化后即可解决,用相同的方式将an>an+1进行转换,设法利用已证结论证明.
【考点精析】认真审题,首先需要了解不等式的证明(不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等).

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】为了解学生的课外阅读时间情况,某学校随机抽取了50人进行统计分析,把这50人每天阅读的时间(单位:分钟)绘制成频数分布表,如下表所示:
阅读时间 |
|
|
|
|
|
|
人数 | 8 | 10 | 12 | 11 | 7 | 2 |
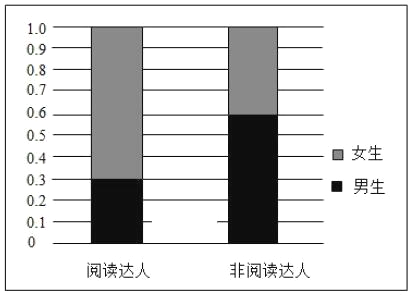
若把每天阅读时间在60分钟以上(含60分钟)的同学称为“阅读达人”,根据统计结果中男女生阅读达人的数据,制作成如图所示的等高条形图.
(1)根据抽样结果估计该校学生的每天平均阅读时间(同一组数据用该区间的终点值作为代表);
(2)根据已知条件完成下面的![]() 列联表,并判断是否有99%的把握认为“阅读达人”跟性别有关?
列联表,并判断是否有99%的把握认为“阅读达人”跟性别有关?
男生 | 女生 | 总计 | |
阅读达人 | |||
非阅读达人 | |||
总计 |
附:参考公式![]() ,其中
,其中![]() .
.
临界值表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某单位招聘员工,有![]() 名应聘者参加笔试,随机抽查了其中
名应聘者参加笔试,随机抽查了其中![]() 名应聘者笔试试卷,统计他们的成绩如下表:
名应聘者笔试试卷,统计他们的成绩如下表:
分数段 |
|
|
|
|
|
|
|
人数 | 1 | 3 | 6 | 6 | 2 | 1 | 1 |
若按笔试成绩择优录取![]() 名参加面试,由此可预测参加面试的分数线为( )
名参加面试,由此可预测参加面试的分数线为( )
A. ![]() 分 B.
分 B. ![]() 分 C.
分 C. ![]() 分 D.
分 D. ![]() 分
分