题目内容
【题目】如图四边形ABCD为菱形,G为AC与BD交点,![]() ,
,
(I)证明:平面![]() 平面
平面![]() ;
;
(II)若![]() ,
,![]() 三棱锥
三棱锥![]() 的体积为
的体积为![]() ,求该三棱锥的侧面积.
,求该三棱锥的侧面积.

【答案】(1)见解析(2)3+2![]()
【解析】试题分析:(Ⅰ)由四边形ABCD为菱形知AC![]() BD,由BE
BD,由BE![]() 平面ABCD知AC
平面ABCD知AC![]() BE,由线面垂直判定定理知AC
BE,由线面垂直判定定理知AC![]() 平面BED,由面面垂直的判定定理知平面
平面BED,由面面垂直的判定定理知平面![]() 平面
平面![]() ;(Ⅱ)设AB=
;(Ⅱ)设AB=![]() ,通过解直角三角形将AG、GC、GB、GD用x表示出来,在
,通过解直角三角形将AG、GC、GB、GD用x表示出来,在![]() AEC中,用x表示EG,在
AEC中,用x表示EG,在![]() EBG中,用x表示EB,根据条件三棱锥
EBG中,用x表示EB,根据条件三棱锥![]() 的体积为
的体积为![]() 求出x,即可求出三棱锥
求出x,即可求出三棱锥![]() 的侧面积.
的侧面积.
试题解析:(Ⅰ)因为四边形ABCD为菱形,所以AC![]() BD,
BD,
因为BE![]() 平面ABCD,所以AC
平面ABCD,所以AC![]() BE,故AC
BE,故AC![]() 平面BED.
平面BED.
又AC![]() 平面AEC,所以平面AEC
平面AEC,所以平面AEC![]() 平面BED
平面BED
(Ⅱ)设AB=![]() ,在菱形ABCD中,由
,在菱形ABCD中,由![]() ABC=120°,可得AG=GC=
ABC=120°,可得AG=GC=![]()
![]() ,GB=GD=
,GB=GD=![]() .
.
因为AE![]() EC,所以在
EC,所以在![]() AEC中,可得EG=
AEC中,可得EG=![]()
![]() .
.
由BE![]() 平面ABCD,知
平面ABCD,知![]() EBG为直角三角形,可得BE=
EBG为直角三角形,可得BE=![]() .
.
由已知得,三棱锥E-ACD的体积![]() .故
.故![]() =2
=2
从而可得AE=EC=ED=![]() .
.
所以![]() EAC的面积为3,
EAC的面积为3,![]() EAD的面积与
EAD的面积与![]() ECD的面积均为
ECD的面积均为![]() .
.
故三棱锥E-ACD的侧面积为![]() .
.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】为了解学生的课外阅读时间情况,某学校随机抽取了50人进行统计分析,把这50人每天阅读的时间(单位:分钟)绘制成频数分布表,如下表所示:
阅读时间 |
|
|
|
|
|
|
人数 | 8 | 10 | 12 | 11 | 7 | 2 |
若把每天阅读时间在60分钟以上(含60分钟)的同学称为“阅读达人”,根据统计结果中男女生阅读达人的数据,制作成如图所示的等高条形图.
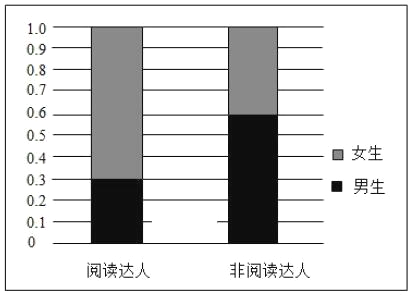
(1)根据抽样结果估计该校学生的每天平均阅读时间(同一组数据用该区间的终点值作为代表);
(2)根据已知条件完成下面的![]() 列联表,并判断是否有99%的把握认为“阅读达人”跟性别有关?
列联表,并判断是否有99%的把握认为“阅读达人”跟性别有关?
男生 | 女生 | 总计 | |
阅读达人 | |||
非阅读达人 | |||
总计 |
附:参考公式![]() ,其中
,其中![]() .
.
临界值表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
