题目内容
【题目】图，从甲地到丙地要经过两个十字路口（十字路口
与十字路口
），从乙地到丙地也要经过两个十字路口（十字路口
与十字路口
），设各路口信号灯工作相互独立，且在，，，路口遇到红灯的概率分别为
，，
，.
（1）求一辆车从乙地到丙地至少遇到一个红灯的概率；
（2）若小方驾驶一辆车从甲地出发，小张驾驶一辆车从乙地出发，他们相约在丙地见面，记
表示这两人见面之前车辆行驶路上遇到的红灯的总个数，求的分布列及数学期望.
【答案】(1)
.
(2)分布列见解析；
.
【解析】分析：（1）根据独立事件的概率计算，可求得都没有遇到红灯的概率，由对立事件的概率求得至少遇到一个红灯的概率。
（2）根据条件可知，遇到红灯个数的分布为
，
，
，
，
，根据概率可分别求得其概率值，列出分布列，由数学期望的计算公式求得的值。
详解：（1）∵一辆车从乙地到丙地没有遇到一个红灯的概率为
，
∴一辆车从乙地到丙地至少遇到一个红灯的概率为
.
（2）
的可能取值为，，，，，
，
，
，
，
，
∴的分布列为
|
|
|
|
|
|
|
|
|
|
|
|
∴
.
练习册系列答案
相关题目
【题目】为了解学生的课外阅读时间情况，某学校随机抽取了50人进行统计分析，把这50人每天阅读的时间（单位：分钟）绘制成频数分布表，如下表所示：
阅读时间 |
|
|
|
|
|
|
人数 | 8 | 10 | 12 | 11 | 7 | 2 |
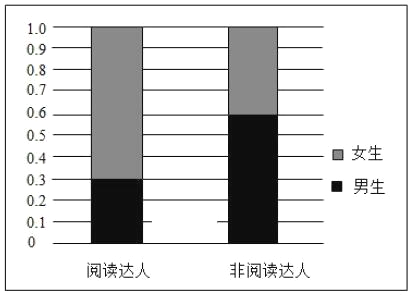
若把每天阅读时间在60分钟以上（含60分钟）的同学称为“阅读达人”，根据统计结果中男女生阅读达人的数据，制作成如图所示的等高条形图.
（1）根据抽样结果估计该校学生的每天平均阅读时间（同一组数据用该区间的终点值作为代表）；
（2）根据已知条件完成下面的
列联表，并判断是否有99%的把握认为“阅读达人”跟性别有关？
男生 | 女生 | 总计 | |
阅读达人 | |||
非阅读达人 | |||
总计 |
附：参考公式
，其中
.
临界值表：
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
