题目内容
1.已知F1,F2分别为椭圆x2a2+y2b2=1(a>b>0)左、右焦点,点P(1,y0)在椭圆上,且PF2⊥x轴,△PF1F2的周长为6;(1)求椭圆的标准方程;
(2)E、F是曲线C上异于点P的两个动点,如果直线PE与直线PF的倾斜角互补,证明:直线EF的斜率为定值,并求出这个定值.
分析 (1)利用点P(1,y0)在椭圆上,且PF2⊥x轴,△PF1F2的周长为6,求出a,b,c,即可求椭圆的标准方程;
(2)设直线PE方程代入椭圆方程,得(3+4k2)x2+4k(3-2k)x+4(32-k)2-12=0,求出E,F的坐标,由此能证明直线EF的斜率为定值.
解答 解:(1)由题意,F1(-1,0),F2(1,0),c=1,…(1分)
C△=|PF1|+|PF2|+2c=2a+2c=8…(2分)
∴a=2,b=√3…(3分)
∴椭圆方程为x24+y23=1…(4分)
(2)由(1)知P(1,32),设直线PE方程:得y=k(x-1)+32,代入x24+y23=1,
得(3+4k2)x2+4k(3-2k)x+4(32-k)2-12=0…(6分)
设E(xE,yE),F(xF,yF).
∵点P(1,32)在椭圆上,
∴xE=4(32−k)2−123+4k2,yE=kxE+32-k,…(12分)
又直线PF的斜率与PE的斜率互为相反数,在上式中以-k代k,
可得xF=4(32+k)2−123+4k2,yF=-kxF+32+k,…(13分)
∴直线EF的斜率kEF=yF−yExF−xE=12.
即直线EF的斜率为定值,其值为12…(15分)
点评 本题考查椭圆方程的求法,考查直线EF的斜率为定值的证明,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
20.若a、b、c∈R,a>b,则下列不等式成立的是( )
| A. | 1a<1b | B. | a2>b2 | C. | ac2+1>bc2+1 | D. | |a|>|b| |
11.公元前3世纪,古希腊欧几里得在《几何原本》里提出:“球的体积(V)与它的直径(D)的立方成正比”,此即V=kD3,欧几里得未给出k的值.17世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式V=kD3中的常数k称为“立圆率”或“玉积率”.类似地,对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式V=kD3求体积(在等边圆柱中,D表示底面圆的直径;在正方体中,D表示棱长).假设运用此体积公式求得球(直径为a)、等边圆柱(底面圆的直径为a)、正方体(棱长为a)的“玉积率”分别为k1、k2、k3,那么k1:k2:k3( )
| A. | 14:16:1π | B. | π6:π4:2 | C. | 2:3:2π | D. | π6:π4:1 |
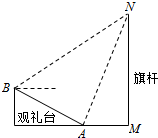 2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10(
2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10( 已知椭圆C1:
已知椭圆C1: