题目内容
15. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上的点到它的两个焦点的距离之和为4,以椭圆C的短轴为直径的圆O经过这两个焦点,点A,B分别是椭圆C的左、右顶点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上的点到它的两个焦点的距离之和为4,以椭圆C的短轴为直径的圆O经过这两个焦点,点A,B分别是椭圆C的左、右顶点.(Ⅰ)求圆O和椭圆C的方程;
(Ⅱ)已知P,Q分别是椭圆C和圆O上的动点(P,Q位于y轴两侧),且直线PQ与x轴平行,直线AP,BP分别与y轴交于点M,N.求证:∠MQN为定值.
分析 (Ⅰ)由椭圆的定义可得a=2,由题意可得b=c,结合椭圆的a,b,c的关系,解方程可得b,c,进而得到圆和椭圆的方程;
(Ⅱ)方法一:设出P的坐标,得到Q的坐标,代入圆和椭圆方程,由AP和BP的方程,求得M,N的坐标,再由向量QM,QN,运用数量积的坐标表示,即可证得∠MQN为定值.
方法二、设P(x0,y0),AP:y=k(x+2)(k≠0).联立椭圆方程,求得P的坐标,进而得到Q,M的坐标,再由BP的方程得到N的坐标,再由向量的数量积的坐标表示,即可得证.
解答 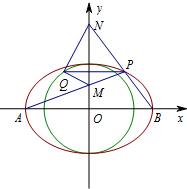 解:(Ⅰ)依题意得$\left\{\begin{array}{l}2a=4\\ c=b\\{a^2}-{b^2}={c^2}.\end{array}\right.$解得:a=2,$b=c=\sqrt{2}$.
解:(Ⅰ)依题意得$\left\{\begin{array}{l}2a=4\\ c=b\\{a^2}-{b^2}={c^2}.\end{array}\right.$解得:a=2,$b=c=\sqrt{2}$.
所以圆O的方程为x2+y2=2,椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$.
(Ⅱ)证法一:如图所示,设P(x0,y0)(y0≠0),Q(xQ,y0),则$\left\{\begin{array}{l}\frac{x_0^2}{4}+\frac{y_0^2}{2}=1\\ x_Q^2+y_0^2\;\;=2\end{array}\right.$即$\left\{\begin{array}{l}x_0^2=4-2y_0^2\\ x_Q^2=2-y_0^2.\end{array}\right.$,
又由$AP:y=\frac{y_0}{{{x_0}+2}}(x+2)$得$M(0,\frac{{2{y_0}}}{{{x_0}+2}})$.
由$BP:y=\frac{y_0}{{{x_0}-2}}(x-2)$得$N(0,-\frac{{2{y_0}}}{{{x_0}-2}})$.
所以 $\overrightarrow{QM}=(-{x_Q},\frac{{2{y_0}}}{{{x_0}+2}}-{y_0})=(-{x_Q},-\frac{{{x_0}{y_0}}}{{{x_0}+2}})$,$\overrightarrow{QN}=(-{x_Q},-\frac{{2{y_0}}}{{{x_0}-2}}-{y_0})=(-{x_Q},-\frac{{{x_0}{y_0}}}{{{x_0}-2}})$.
所以 $\overrightarrow{QM}•\overrightarrow{QN}=x_Q^2+\frac{x_0^2y_0^2}{x_0^2-4}=2-y_0^2+\frac{(4-2y_0^2)y_0^2}{-2y_0^2}=0$.
所以 QM⊥QN,即∠MQN=90°.
(Ⅱ)证法二:如图所示,设P(x0,y0),AP:y=k(x+2)(k≠0).
由$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{2}=1\\ y=k(x+2)\end{array}\right.$得(2k2+1)x2+8k2x+8k2-4=0.
所以 $-2{x_0}=\frac{{8{k^2}-4}}{{2{k^2}+1}}$,即${x_0}=\frac{{2-4{k^2}}}{{2{k^2}+1}}$.
所以 ${y_0}=\frac{4k}{{2{k^2}+1}}$,即$P(\frac{{2-4{k^2}}}{{2{k^2}+1}},\frac{4k}{{2{k^2}+1}})$.
所以 直线BP的斜率为$\frac{{\frac{4k}{{2{k^2}+1}}}}{{\frac{{2-4{k^2}}}{{2{k^2}+1}}-2}}=-\frac{1}{2k}$.
所以 $BP:y=-\frac{1}{2k}(x-2)$.
令x=0得:M(0,2k),$N(0,\frac{1}{k})$.
设Q(xQ,y0),则$\overrightarrow{QM}=(-{x_Q},2k-{y_0})$,$\overrightarrow{QN}=(-{x_Q},\frac{1}{k}-{y_0})$.
所以 $\overrightarrow{QM}•\overrightarrow{QN}=x_Q^2+(2k-{y_0})(\frac{1}{k}-{y_0})=x_Q^2+y_0^2+2-\frac{{2{k^2}+1}}{k}•{y_0}$.
因为 $x_Q^2+y_0^2=2,{y_0}=\frac{4k}{{2{k^2}+1}}$,
所以 $\overrightarrow{QM}•\overrightarrow{QN}=0$.
所以 QM⊥QN,即∠MQN=90°.
点评 本题考查椭圆的定义、方程和性质,主要考查椭圆的定义和方程的运用,联立直线方程和圆的方程,运用韦达定理和向量垂直的条件,考查运算能力,属于中档题.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案| A. | 若{dn}满足dn=$\frac{{{b_1}+2{b_2}+3{b_3}+…+n{b_n}}}{1+2+3+…n}$,则{dn}也是等比数列 | |
| B. | 若{dn}满足dn=$\frac{{{b_1}•2{b_2}•3{b_3}•…•n{b_n}}}{1•2•3•…•n}$,则{dn}也是等比数列 | |
| C. | 若{dn}满足${d_n}={[{b_1}•(2{b_2})•(3{b_3})•…•(n{b_n})]^{\frac{1}{1+2+…+n}}}$,则{dn}也是等比数列 | |
| D. | 若{dn}满足${d_n}={[{b_1}•{b_2}^2•{b_3}^3•…•{b_n}^n]^{\frac{1}{1+2+…+n}}}$,则{dn}也是等比数列 |
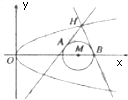 如图,已知⊙M:(x-4)2+y2=1和抛物线C:y2=2px(p>0,其焦点为F),且$\overrightarrow{FM}$=($\frac{15}{4}$,0,),过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切于A、B两点.
如图,已知⊙M:(x-4)2+y2=1和抛物线C:y2=2px(p>0,其焦点为F),且$\overrightarrow{FM}$=($\frac{15}{4}$,0,),过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切于A、B两点. 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A(1,$\frac{\sqrt{2}}{2}$),其焦距为2.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A(1,$\frac{\sqrt{2}}{2}$),其焦距为2. 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,且AC=BC=CC1=2,M是AB1与A1B的交点,N是B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,且AC=BC=CC1=2,M是AB1与A1B的交点,N是B1C1的中点.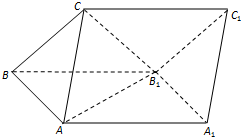 如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.