题目内容
14.已知点A(1,4),B(4,1),直线L:y=ax+2与线段AB相交于P,则a的范围[$-\frac{1}{4}$,2].分析 根据直线斜率公式,进行求解即可得到结论.
解答 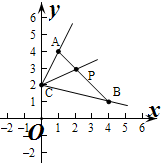 解:作出对应的图象如图:
解:作出对应的图象如图:
若直线L:y=ax+2与线段AB相交于P,
直线y=ax+2过定点C(0,2),
则满足kCB≤kCp≤kCA,
∵kCB=$\frac{1-2}{4-0}$=$-\frac{1}{4}$,kCA=$\frac{4-2}{1-0}$=2,
即$-\frac{1}{4}$≤kCp≤2,
即$-\frac{1}{4}$≤a≤2,
故答案为:[$-\frac{1}{4}$,2]
点评 本题主要考查直线方程和直线斜率的应用,利用数形结合是解决本题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
4.已知cosα=$\frac{4}{5}$,α∈(-$\frac{π}{2}$,0),则tan($\frac{π}{4}$+$\frac{α}{2}$)的值是( )
| A. | 2 | B. | $\frac{2}{5}$ | C. | -2 | D. | -$\frac{1}{2}$ |
5.一个算法的程序框图如图所示,若运行该程序后输出的结果为$\frac{4}{5}$,则判断框中应填入的条件是( )
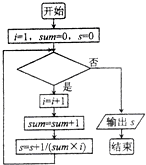

| A. | i≤5? | B. | i≤4? | C. | i≥4? | D. | i≥5? |
2.若函数y=f(x)是函数y=($\frac{1}{2}$)x的反函数,则f(4)=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
19.已知实数a,b,c满足不等式0<a<b<c<1,且M=2a,N=5-b,P=$(\frac{1}{7}{)^c}$,则M、N、P的大小关系为( )
| A. | M>N>P | B. | P<M<N | C. | N>P>M | D. | P>N>M |
6.设a>0,b>0,若$\sqrt{3}$是93a与3b的等比中项,则$\frac{2}{a}+\frac{1}{b}$的最小值为( )
| A. | 1 | B. | 13+$4\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{13}{2}+2\sqrt{3}$ |