题目内容
4.已知函数f(x)=$\frac{(x-a)^{2}}{lnx}$(其中a为常数).(Ⅰ)当a=0时,求函数的单调区间;
(Ⅱ)当a<1时,若在区间(1,2)上存在不相等的实数m,n,使f(m)=f(n)成立,求a的取值范围;
(Ⅲ)当a=1时,对于任意大于1的实数x,恒有f(x)≥k成立,求实数k的取值范围.
分析 (Ⅰ)先求出函数的导数,解关于导函数的不等式,从而求出函数的单调区间;
(Ⅱ)问题转化为求使函数f(x)在(1,2)上不为单调函数的a的取值范围,通过讨论x的范围,得到函数的单调性,进而求出a的范围;
(Ⅲ)x>1时,f(x)≥k,即(x-1)2-klnx≥0成立,分类讨论利用函数的单调性即可求出实数k的范围.
解答 解:(Ⅰ)a=0时,f(x)=$\frac{{x}^{2}}{lnx}$,f′(x)=$\frac{x(2lnx-1)}{{(lnx)}^{2}}$,
令f′(x)>0,解得:x>$\sqrt{e}$,令f′(x)<0,解得:0<x<$\sqrt{e}$,
∴函数f(x)在(0,$\sqrt{e}$)递减,在($\sqrt{e}$,+∞)递增;
(Ⅱ)依题意即求使函数f(x)=$\frac{{(x-a)}^{2}}{lnx}$在(1,2)上不为单调函数的a的取值范围,
而f′(x)=$\frac{(x-a)[2xlnx-(x-a)]}{{x(lnx)}^{2}}$,(1<x<2,a<1),
设g(x)=2xlnx-x+a,则g(1)=a-1,g(2)=4ln2-2+a,
因为g′(x)=2lnx+1>0,g(x)在(1,2)上为增函数,
当$\left\{\begin{array}{l}{g(1)=a-1<0}\\{g(2)=4ln2-2+a>0}\end{array}\right.$,即当2-4ln2<a<1时,函数g(x)在(1,2)上有且只有一个零点,设为x0,
当x∈(1,x0)时,g(x)<0,即f′(x)<0,f(x)为减函数;
当x∈(x0,2)时,g(x)>0,即f′(x)>0,f(x)为增函数,满足在(1,2)上不为单调函数.
当a≤2-4ln2时,g(1)<0,g(2)<0,所以在(1,2)上g(x)<0成立(因g(x)在(1,2)上为增函数),
所以在(1,2)上f′(x)<0成立,即f(x)在(1,2)上为减函数,不合题意,
综上:2-4ln2<a<1.
(Ⅲ)x>1时,f(x)≥k,即(x-1)2-klnx≥成立,
令g(x)=(x-1)2-klnx,则g′(x)=$\frac{{2x}^{2}-2x-k}{x}$,
∵x>1,∴2x2-2x=2x(x-1)>0,
①k≤0,g′(x)>0,∴g(x)在(1,+∞)单调递增,
∴x>1时,g(x)>g(1)=0,满足题意,
②k>0时,令f′(x)=0,解得:x1=$\frac{1-\sqrt{1+2k}}{2}$<0,x2=$\frac{1+\sqrt{1+2k}}{2}$>1,
∴x∈(1,x2),g′(x)<0,g(x)在(1,x2)单调递减,
∴x∈(1,x2)时,g(x)<g(1)=0(舍),
∴k≤0.
点评 本题考查了函数的单调性,函数的极值问题,导数的应用,考查转化思想,分类讨论思想,熟练掌握基础知识并对其灵活应用是解题的关键,本题是一道难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | y=cos2x | B. | y=sin2x | C. | y=|cosx| | D. | y=|sinx| |
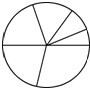 一个圆分成6个大小不等的小扇形,取来红、黄、蓝、白、绿、黑6种颜色,如图.
一个圆分成6个大小不等的小扇形,取来红、黄、蓝、白、绿、黑6种颜色,如图.