题目内容
9.已知中心在原点的椭圆C的右焦点为($\sqrt{3}$,0),离心率e=$\frac{\sqrt{3}}{2}$(1)求椭圆C的标准方程;
(2)设过椭圆左顶点A的直线l交椭圆于另一点B,且AB中点横坐标为$-\frac{8}{5}$,求l的方程.
分析 (1)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得c=$\sqrt{3}$,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,结合a,b,c的关系,解得a=2,b=1,进而得到椭圆方程;
(2)设直线l:y=k(x+2),代入椭圆方程,消去y,运用韦达定理和中点坐标公式,即可得到k,进而得到直线l的方程.
解答 解:(1)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得c=$\sqrt{3}$,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
解得a=2,b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
即有椭圆方程为$\frac{{x}^{2}}{4}$+y2=1;
(2)A(-2,0),设直线l:y=k(x+2),
代入椭圆方程可得,(1+4k2)x2+16k2x+16k2-4=0,
则-2+xB=-$\frac{16{k}^{2}}{1+4{k}^{2}}$,
由AB中点横坐标为$-\frac{8}{5}$,可得-$\frac{16{k}^{2}}{1+4{k}^{2}}$=-$\frac{16}{5}$,
解得k=±1,
检验判别式(16k2)2-4(1+4k2)(16k2-4)=16>0,成立.
则有直线l的方程为y=x+2或y=-x-2.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,联立直线方程,运用韦达定理和中点坐标公式,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
1.一只小狗在如图所示的方砖上走来走去,求最终停在阴影方砖上的概率为( )
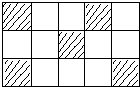

| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |