题目内容
已知中心在原点,对称轴为坐标轴的椭圆与直线x+y=3相交于A、B两点,C是AB的中点,若|AB|=2 ,O是坐标原点,OC的斜率为2,求椭圆的方程.
,O是坐标原点,OC的斜率为2,求椭圆的方程.
 ,O是坐标原点,OC的斜率为2,求椭圆的方程.
,O是坐标原点,OC的斜率为2,求椭圆的方程.a>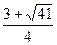 .
.
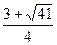 .
.思路分析一:本题涉及弦长、弦的中点,可以将弦长公式与点差法综合运用解决问题.
设椭圆方程为mx2+ny2=1(m>0,n>0),A(x1,y1)、B(x2,y2)、C(x0,y0),
则mx12+ny12=1,mx22+ny22=1.
两式相减得m(x1+x2)(x1-x2)+n(y1+y2)(y1-y2)=0.
∴kAB=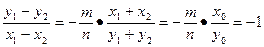 .
.
又∵kOC=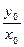 =2,∴
=2,∴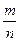 =2,即m=2n.
=2,即m=2n.
将y=3-x代入椭圆方程mx2+ny2=1,得(m+n)x2-6nx+9n-1=0.
由弦长公式得|AB|=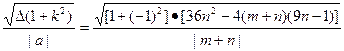
=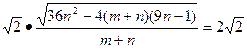 .
.
将m=2n代入得n=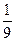 ,m=
,m=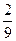 .
.
故所求椭圆方程为2x2+y2=9.
设椭圆方程为mx2+ny2=1(m>0,n>0),A(x1,y1)、B(x2,y2)、C(x0,y0),
则mx12+ny12=1,mx22+ny22=1.
两式相减得m(x1+x2)(x1-x2)+n(y1+y2)(y1-y2)=0.
∴kAB=
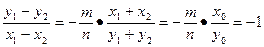 .
.又∵kOC=
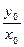 =2,∴
=2,∴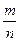 =2,即m=2n.
=2,即m=2n.将y=3-x代入椭圆方程mx2+ny2=1,得(m+n)x2-6nx+9n-1=0.
由弦长公式得|AB|=
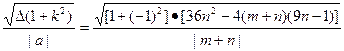
=
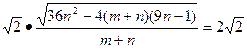 .
.将m=2n代入得n=
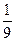 ,m=
,m=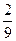 .
.故所求椭圆方程为2x2+y2=9.

练习册系列答案
相关题目
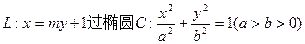 的右焦点F,且交椭圆C于A,B两点,点A,F,B在直线
的右焦点F,且交椭圆C于A,B两点,点A,F,B在直线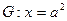 上的射影依次为点D,K,E.
上的射影依次为点D,K,E.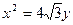 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;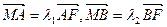 ,当m变化时,求
,当m变化时,求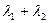 的值;
的值;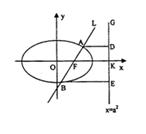
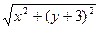 +
+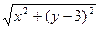 =10为不含根式的形式是( )
=10为不含根式的形式是( )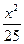 +
+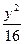 ="1"
="1"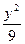 =1
=1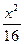 +
+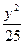 ="1"
="1"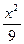 +
+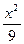 +
+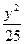 =1上到两个焦点距离之积最大的点的坐标是_______________.
=1上到两个焦点距离之积最大的点的坐标是_______________.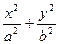 =1(a>b>0)的内接矩形面积的最大值.
=1(a>b>0)的内接矩形面积的最大值.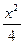 +y2=1相交于A、B两点,当t变化时,|AB|的最大值为( )
+y2=1相交于A、B两点,当t变化时,|AB|的最大值为( ) C.
C. D.
D.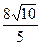
 ;
; ;
; .
. =1的准线平行于x轴,则实数m的取值范围是( )
=1的准线平行于x轴,则实数m的取值范围是( ) <m<3且m≠0
<m<3且m≠0 +
+ ="1" (a>b>0)的两准线间的距离为
="1" (a>b>0)的两准线间的距离为 ,离心率为
,离心率为 ,则椭圆的方程为( )
,则椭圆的方程为( ) +
+ ="1"
="1"  +
+ ="1"
="1" =1
=1