题目内容
若直线y=x+t与椭圆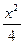 +y2=1相交于A、B两点,当t变化时,|AB|的最大值为( )
+y2=1相交于A、B两点,当t变化时,|AB|的最大值为( )
A.2 B. C.
C. D.
D.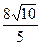
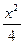 +y2=1相交于A、B两点,当t变化时,|AB|的最大值为( )
+y2=1相交于A、B两点,当t变化时,|AB|的最大值为( )A.2 B.
 C.
C. D.
D.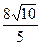
C
联立两个方程化为
5x2+8tx+4t2-4=0.
设A(x1,y1)、B(x2,y2),则x1+x2=- t,x1x2=
t,x1x2= (t2-1).
(t2-1).
|AB|=
=
 .
.
而Δ=(8t)2-4×5×(4t2-4)>0,
解得0≤t2<5.
∴取t2=0得|AB|最大=
 .
.
5x2+8tx+4t2-4=0.
设A(x1,y1)、B(x2,y2),则x1+x2=-
 t,x1x2=
t,x1x2= (t2-1).
(t2-1).|AB|=

=

 .
.而Δ=(8t)2-4×5×(4t2-4)>0,
解得0≤t2<5.
∴取t2=0得|AB|最大=

 .
.
练习册系列答案
相关题目
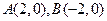 ,
,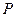 是平面内一动点,直线
是平面内一动点,直线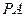 、
、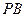 斜率之积为
斜率之积为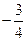 .
. 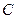 的方程;
的方程;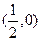 作直线
作直线 与轨迹
与轨迹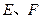 两点,线段
两点,线段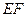 的中点为
的中点为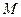 ,求直线
,求直线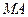 的斜率
的斜率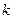 的取值范围.
的取值范围.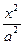 +
+ =1(a>b>0)的左、右焦点,点P在椭圆上,△POF2是面积为
=1(a>b>0)的左、右焦点,点P在椭圆上,△POF2是面积为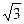 的正三角形,则b2的值是_______________.
的正三角形,则b2的值是_______________. =1(a>b>0)的弦,求这些弦长的最大值.
=1(a>b>0)的弦,求这些弦长的最大值.
 ,O是坐标原点,OC的斜率为2,求椭圆的方程.
,O是坐标原点,OC的斜率为2,求椭圆的方程. +
+ =1相切,则k、a之间的关系式为( )
=1相切,则k、a之间的关系式为( ) +
+ =1的右焦点,M为椭圆上一点,且使|MP|+2|MF|的值最小,则点M为______________.
=1的右焦点,M为椭圆上一点,且使|MP|+2|MF|的值最小,则点M为______________.


 +
+ ="1"
="1" =1
=1 ="1"
="1" =1
=1