题目内容
椭圆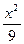
+
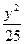=1上到两个焦点距离之积最大的点的坐标是_______________.
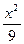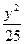+=1上到两个焦点距离之积最大的点的坐标是_______________.M(±3,0)
解法一:两焦点F(0,±4).
设椭圆上任一点M(3cosθ,5sinθ),
∴|MF1|·|MF2|=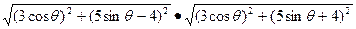
=
=
=
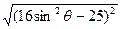
=25-16sin2θ.
取sinθ=0得|MF1|·|MF2|最大=25.
此时M(±3,0).
解法二:|MF1|·|MF2|≤(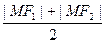
)2=a2.
当且仅当|MF1|=|MF2|即M点为短轴端点(±3,0)时,积最大.
设椭圆上任一点M(3cosθ,5sinθ),
∴|MF1|·|MF2|=
=
=
=
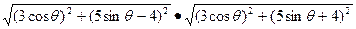
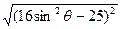
=25-16sin2θ.
取sinθ=0得|MF1|·|MF2|最大=25.
此时M(±3,0).
解法二:|MF1|·|MF2|≤(
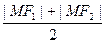)2=a2.当且仅当|MF1|=|MF2|即M点为短轴端点(±3,0)时,积最大.
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
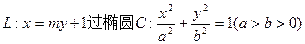的右焦点F，且交椭圆C于A，B两点，点A，F，B在直线
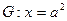上的射影依次为点D，K，E.
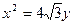的焦点为椭圆C的上顶点，求椭圆C的方程；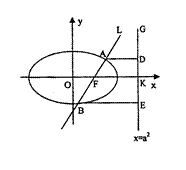
过点
，且焦点为
。
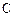的方程；
的动直线
与椭圆
上取点
，
，证明：点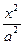
+
=1（a＞b＞0）的左、右焦点，点P在椭圆上，△POF2是面积为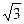
的正三角形，则b2的值是_______________.
=1(a>b>0)的弦,求这些弦长的最大值.
,O是坐标原点,OC的斜率为2,求椭圆的方程.
+
=1的右焦点,M为椭圆上一点,且使|MP|+2|MF|的值最小,则点M为______________.
,1)、P2(-
,-
),求椭圆方程.
的
半焦距等于（ ）
