题目内容
函数f(x)的导函数是f′(x),若对任意的x∈R,都有f(x)+2f′(x)<0成立,则( )
A.
| B.
| ||||||||
C.
| D.无法比较 |
令h(x)=xf(2lnx),则h′(x)=f(2lnx)+xf′(2lnx)•
=f(2lnx)+2f′(2lnx)
∵对任意的x∈R都有f(x)+2f′(x)<0成立,
∴f(2lnx)+2f′(2lnx)<0,
即h′(x)<0,h(x)在定义域上单调递减,
∴h(2)>h(3),即2f(2ln2)>3f(2ln3).
即
>
,
故选:B.
| 2 |
| x |
∵对任意的x∈R都有f(x)+2f′(x)<0成立,
∴f(2lnx)+2f′(2lnx)<0,
即h′(x)<0,h(x)在定义域上单调递减,
∴h(2)>h(3),即2f(2ln2)>3f(2ln3).
即
| f(2ln2) |
| 3 |
| f(2ln3) |
| 2 |
故选:B.

练习册系列答案
相关题目
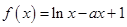 在
在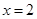 处的切线斜率为
处的切线斜率为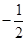 .
. 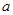 的值及函数
的值及函数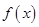 的单调区间;
的单调区间;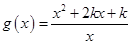 ,对
,对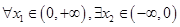 使得
使得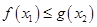 恒成立,求正实数
恒成立,求正实数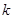 的取值范围;
的取值范围;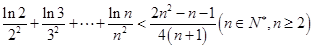 .
.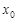 是函数
是函数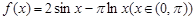 的零点,
的零点,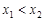 ,则:①
,则:①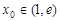 ;②
;②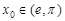 ;
;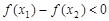 ;④
;④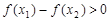 ,其中正确的命题是( )
,其中正确的命题是( )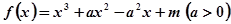
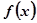 的单调增区间;
的单调增区间;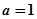 时,函数
时,函数 的取值范围.
的取值范围.