题目内容
（Ⅰ）求函数y=2xcosx的导数；
（Ⅱ）已知A+B=
，且A，B≠kπ+
(k∈Z)．
求证：（1+tanA）（1+tanB）=2．
（Ⅱ）已知A+B=
| 5π |
| 4 |
| π |
| 2 |
求证：（1+tanA）（1+tanB）=2．
（I）由导数的运算法则，可得
y'=（2xcosx）'=（2x）'cosx+2x（cosx）'=2cosx-2xcosx．
即函数y=2xcosx的导数为y'=2cosx-2xcosx；
（II）∵A+B=
，∴tan（A+B）=tan
=1．
即
=1，可得tanA+tanB=1-tanAtanB，
因此（1+tanA）（1+tanB）=1+tanA+tanB+tanAtanB
=1+（1-tanAtanB）+tanAtanB=2．
∴等式（1+tanA）（1+tanB）=2成立．
y'=（2xcosx）'=（2x）'cosx+2x（cosx）'=2cosx-2xcosx．
即函数y=2xcosx的导数为y'=2cosx-2xcosx；
（II）∵A+B=
| 5π |
| 4 |
| 5π |
| 4 |
即
| tanA+tanB |
| 1-tanAtanB |
因此（1+tanA）（1+tanB）=1+tanA+tanB+tanAtanB
=1+（1-tanAtanB）+tanAtanB=2．
∴等式（1+tanA）（1+tanB）=2成立．
练习册系列答案
相关题目
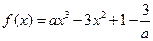.（Ｉ）讨论函数
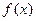的单调性；（Ⅱ）若曲线
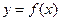上两点A、B处的切线都与
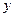轴垂直，且线段AB与
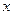轴有公共点，求实数
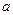的取值范围.
在
上单调递减，在（1，3）上单调递增在
上单调递减，且函数图象在
处的切线与直线
垂直．
、
、
的值；（Ⅱ）设函数
=0有三个不相等的实数根，求
的取值范围．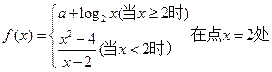
连续，则常数
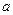的值是( )