题目内容
已知函数f(x)=
,其导函数记为f′(x),则f(2012)+f′(2012)+f(-2012)-f′(-2012)=______.
| (x+1)2+sinx |
| x2+1 |
由题意可得函数f(x)=
=
=1+
,
故其导函数f′(x)=
,
易证f′(-x)=f′(x),故导函数f′(x)为偶函数,所以f'(2012)=f'(-2012);
记函数h(x)=
,显然有h(-x)=-h(x),即h(x)为奇函数,
可得h(-2012)=-h(2012),即h(2012)+h(-2012)=0,
故f(2012)+f'(2012)+f(-2012)-f'(-2012)=f(2012)+f(-2012)
=1+h(2012)+1+h(-2012)=2+h(2012)+h(-2012)=2,
故答案为:2
| (x+1)2+sinx |
| x2+1 |
| x2+1+2x+sinx |
| x2+1 |
| 2x+sinx |
| x2+1 |
故其导函数f′(x)=
| (2+cosx)(x2+1)-(2x+sinx)(2x) |
| (x2+1)2 |
易证f′(-x)=f′(x),故导函数f′(x)为偶函数,所以f'(2012)=f'(-2012);
记函数h(x)=
| 2x+sinx |
| x2+1 |
可得h(-2012)=-h(2012),即h(2012)+h(-2012)=0,
故f(2012)+f'(2012)+f(-2012)-f'(-2012)=f(2012)+f(-2012)
=1+h(2012)+1+h(-2012)=2+h(2012)+h(-2012)=2,
故答案为:2

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
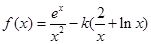 (
(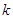 为常数,
为常数,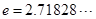 是自然对数的底数).
是自然对数的底数).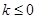 时,求函数
时,求函数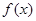 的单调区间;
的单调区间;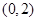 内存在两个极值点,求
内存在两个极值点,求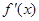 ,且满足
,且满足 ,则
,则 与
与 的大小关系为( ).
的大小关系为( ).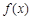 ,若对任意
,若对任意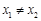 ,都有
,都有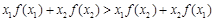 ,则称f(x)为“H函数”,给出下列函数:①
,则称f(x)为“H函数”,给出下列函数:①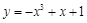 ;②
;② ;③
;③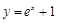 ;④
;④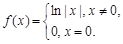 其中是“H函数”的个数为
其中是“H函数”的个数为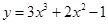 在区间
在区间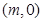 上为减函数, 则
上为减函数, 则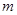 的取值范围是__ ___.
的取值范围是__ ___.