题目内容
19.已知三角形ABC中,点A,B的坐标分别为A(3,0),B(0,3),若点C(1,t),∠B是钝角,则t的取值范围为t>4.分析 因为∠B是钝角,所以$\overrightarrow{BC}•\overrightarrow{BA}<0$,即3-3(t-3)<0,解得t>4.
解答 解:∵A(3,0),B(0,3),C(1,t)
∴$\overrightarrow{BC}$=(1,t-3),$\overrightarrow{BA}$=(3,-3)
∵∠B是钝角,∴$\overrightarrow{BC}•\overrightarrow{BA}<0$,即3-3(t-3)<0,解得t>4,
故答案为:t>4.
点评 本题考查了平面向量在三角形中的应用,属于基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
10.在△ABC中,已知a=40,b=20$\sqrt{2}$,A=45°,则角B等于( )
| A. | 60° | B. | 60°或120° | C. | 30° | D. | 30°或150° |
7.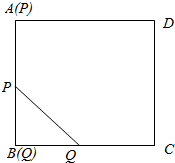 如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
 如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )| A. | 0 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
4.设$\overrightarrow{a}$=(x,2y,3),$\overrightarrow{b}$=(1,1,6),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则x+y等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |