题目内容
9.求y=$\frac{6\sqrt{{x}^{2}+1}}{{x}^{2}+4}$的最大值.分析 换元,利用基本不等式,即可得出结论.
解答 解:设$\sqrt{{x}^{2}+1}$=t(t≥1),则y=$\frac{6t}{{t}^{2}+3}$=$\frac{6}{t+\frac{3}{t}}$≤$\frac{6}{2\sqrt{t•\frac{3}{t}}}$=$\sqrt{3}$,
当且仅当t=$\sqrt{3}$时取等号,所以y=$\frac{6\sqrt{{x}^{2}+1}}{{x}^{2}+4}$的最大值为$\sqrt{3}$.
点评 本题考查函数的最大值,考查换元法的运用,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
3.已知复数z=x+yi(x,y∈R),且|z-2|=$\sqrt{3}$,则$\frac{y+1}{x}$的最大值为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | 2+$\sqrt{6}$ | D. | 2-$\sqrt{6}$ |
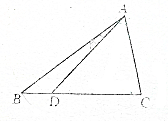 如图,在直角三角形ABC中,∠C=90°,D为BC边上的一点,且BC=4BD,设∠CAD=α,∠BAD=β,若tanα=7tanβ,求角α的大小.
如图,在直角三角形ABC中,∠C=90°,D为BC边上的一点,且BC=4BD,设∠CAD=α,∠BAD=β,若tanα=7tanβ,求角α的大小.