题目内容
“a=1”是“函数f（x）=|x-a|+b（a，b∈R）在区间[1，+∞）上为增函数”的（ ）
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：函数的性质及应用,简易逻辑
分析：根据函数的单调性的性质，利用充分条件和必要条件的定义进行判断即可得到结论．
解答：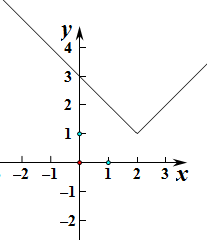
解：当a=1时，f（x）=|x-1|+b在[1，+∞）上为增函数；
反之，f（x）=|x-1|+b在区间[1，+∞）上为增函数，则a≤1，
故“a=1”是“函数f（x）=|x-a|+b（a，b∈R）在区间[1，+∞）上为增函数”的充分不必要条件，
故选：A．
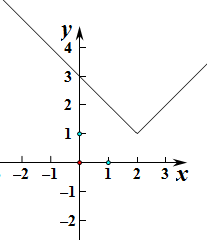解：当a=1时，f（x）=|x-1|+b在[1，+∞）上为增函数；反之，f（x）=|x-1|+b在区间[1，+∞）上为增函数，则a≤1，
故“a=1”是“函数f（x）=|x-a|+b（a，b∈R）在区间[1，+∞）上为增函数”的充分不必要条件，
故选：A．
点评：本题主要考查充分条件和必要条件的判断，利用三角函数的图象和性质是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若{bn}为等差数列，b2=4，b4=8．数列{an}满足a1=1，bn=an+1-an（n∈N*），则a8=（ ）
| A、56 | B、57 | C、72 | D、73 |
若p：φ=
+kπ，k∈Z，q：f（x）=sin（ωx+φ）（ω≠0）是偶函数，则p是q的（ ）
| π |
| 2 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
已知a，b∈R，则“log2a＞log2b”是“(
)a＜(
)b”的（ ）
| 1 |
| 3 |
| 1 |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知椭圆C：
+
=1（a＞b＞0）的左、右焦点为F1、F2，离心率为
，过F2的直线l交C于A、B两点，若△AF1B的周长为4
，则C的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知M是x2=8y的对称轴与准线的交点，点N是其焦点，点P在该抛物线上，且满足|PM|=m|PN|，当m取得最大值时，点P恰在以M、N为焦点的双曲线上，则该双曲线的实轴长为（ ）
A、2（
| ||
B、4（
| ||
C、2（
| ||
D、4（
|
某班级开会时决定是否增加一名新班委甲某，选举方式最能体现全体学生的真实意愿的是（ ）
| A、请同意增选甲为新班委的举手 | B、请不同意增选甲为新班委的举手 | C、采用无记名投票 | D、采用记名投票 |