题目内容
以下命题中，真命题有（ ）
①已知平面α、β和直线m，若m∥α且α⊥β，则m⊥β．
②“若x2＜1，则-1＜x＜1”的逆否命题是“若x＜-1或x＞1，则x2＞1”．
③已知△ABC，D为AB边上一点，若
=2
，
=
+λ
，则λ=
．
④着实数x，y满足约束条件
，则z=2x-y的最大值为2．
①已知平面α、β和直线m，若m∥α且α⊥β，则m⊥β．
②“若x2＜1，则-1＜x＜1”的逆否命题是“若x＜-1或x＞1，则x2＞1”．
③已知△ABC，D为AB边上一点，若
| AD |
| DB |
| CD |
| 1 |
| 3 |
| CA |
| CB |
| 2 |
| 3 |
④着实数x，y满足约束条件
|
| A、0个 | B、1个 | C、2个 | D、3个 |
考点：命题的真假判断与应用
专题：简易逻辑
分析：对于①，由空间中的线面关系判断真假；
对于②，写出原命题的逆否命题判断真假；
对于③，通过画图把
用
与
线性表示，则λ值可求；
对于④，由约束条件作出可行域，求得最优解的坐标，代入目标函数求得最大值．
对于②，写出原命题的逆否命题判断真假；
对于③，通过画图把
| CD |
| CA |
| CB |
对于④，由约束条件作出可行域，求得最优解的坐标，代入目标函数求得最大值．
解答：解：对于①，m∥α且α⊥β，则m与β的位置关系可能有如下几种情况：
m?β或m∥β或m与β相交．命题①是假命题；
对于②，“若x2＜1，则-1＜x＜1”的逆否命题是“若x≤-1或x≥1，则x2≥1”．
命题②是假命题；
对于③，如图，
∵
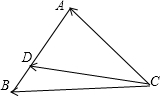
=2
，
∴
=
+
=
+
=
+
(
-
)=
+
，
又
=
+λ
，
∴λ=
．命题③是真命题；
对于④，由约束条件
作可行域如图，
联立
，解得A（2，2）．
∴z=2x-y的最大值为2．命题④是真命题．
∴真命题有2个．
故选：C．
m?β或m∥β或m与β相交．命题①是假命题；
对于②，“若x2＜1，则-1＜x＜1”的逆否命题是“若x≤-1或x≥1，则x2≥1”．
命题②是假命题；
对于③，如图，
∵
| AD |
| DB |
∴
| CD |
| CA |
| AD |
| CA |
| 2 |
| 3 |
| AB |
| CA |
| 2 |
| 3 |
| CB |
| CA |
| 1 |
| 3 |
| CA |
| 2 |
| 3 |
| CB |
又
| CD |
| 1 |
| 3 |
| CA |
| CB |
∴λ=
| 2 |
| 3 |
对于④，由约束条件
|
联立
|
∴z=2x-y的最大值为2．命题④是真命题．
∴真命题有2个．
故选：C．
点评：本题考查了命题的真假判断与应用，考查了平面向量的应用，训练了利用线性规划求目标函数的最值，是中档题．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知f（x）=sinπx+cos（πx-
），则f（x）具有性质是（ ）
| π |
| 6 |
A、图象的一个对称中心为（
| ||
B、图象的一个对称轴为直线x=
| ||
| C、最小正周期为1 | ||
| D、最大值为2，最小值为-2 |
已知命题p：函数y=sin4x是最小正周期为
的周期函数，命题q：函数y=tanx在（
，π）上单调递减，则下列命题为真命题的是（ ）
| π |
| 2 |
| π |
| 2 |
| A、p∧q |
| B、（￢p）∨q |
| C、（￢p）∧（￢q） |
| D、（￢p）∨（￢q） |
下列命题是假命题的是（ ）
| A、?α，β∈R，使tan（α+β）=tanα+tanβ成立 | B、?α，β∈R，使cos（α+β）＜cosα+cosβ成立 | C、△ABC中，“A＜B”是“sinA＜sinB”成立的充要条件 | D、?φ∈R，函数y=sin（2x+φ）都不是偶函数 |
已知集合A={x|x2-3x+2≤0}，B={x|
＞0，a＞0}，若“x∈A”是“x∈B”的充分非必要条件，则a的取值范围是（ ）
| x-a |
| x+2 |
| A、0＜a＜1 | B、a≥2 |
| C、1＜a＜2 | D、a≥1 |
“a=1”是“函数f（x）=|x-a|+b（a，b∈R）在区间[1，+∞）上为增函数”的（ ）
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |