题目内容
已知M是x2=8y的对称轴与准线的交点,点N是其焦点,点P在该抛物线上,且满足|PM|=m|PN|,当m取得最大值时,点P恰在以M、N为焦点的双曲线上,则该双曲线的实轴长为( )
A、2(
| ||
B、4(
| ||
C、2(
| ||
D、4(
|
考点:抛物线的简单性质,双曲线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:过P作准线的垂线,垂足为B,则由抛物线的定义,结合|PM|=m|PN|,可得
=
,设PM的倾斜角为α,则当m取得最大值时,sinα最小,此时直线PM与抛物线相切,求出P的坐标,利用双曲线的定义,即可得出结论.
| 1 |
| m |
| |PB| |
| |PM| |
解答: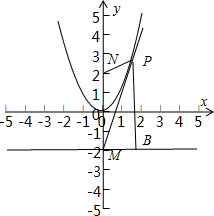 解:过P作准线的垂线,垂足为B,则由抛物线的定义可得|PN|=|PB|,
解:过P作准线的垂线,垂足为B,则由抛物线的定义可得|PN|=|PB|,
∵|PM|=m|PN|,
∴|PM|=m|PB|
∴
=
,
设PM的倾斜角为α,则sinα=
,
当m取得最大值时,sinα最小,此时直线PM与抛物线相切,
设直线PM的方程为y=kx-2,代入x2=8y,可得x2=8(kx-2),
即x2-8kx+16=0,
∴△=64k2-64=0,
∴k=±1,
∴P(4,4
),
∴双曲线的实轴长为PM-PN=
-(4
+2)=4(
-1).
故选:B.
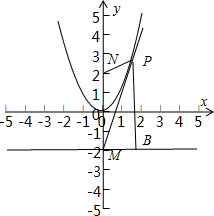 解:过P作准线的垂线,垂足为B,则由抛物线的定义可得|PN|=|PB|,
解:过P作准线的垂线,垂足为B,则由抛物线的定义可得|PN|=|PB|,∵|PM|=m|PN|,
∴|PM|=m|PB|
∴
| 1 |
| m |
| |PB| |
| |PM| |
设PM的倾斜角为α,则sinα=
| 1 |
| m |
当m取得最大值时,sinα最小,此时直线PM与抛物线相切,
设直线PM的方程为y=kx-2,代入x2=8y,可得x2=8(kx-2),
即x2-8kx+16=0,
∴△=64k2-64=0,
∴k=±1,
∴P(4,4
| 2 |
∴双曲线的实轴长为PM-PN=
14+(4
|
| 2 |
| 2 |
故选:B.
点评:本题考查抛物线的性质,考查双曲线、抛物线的定义,考查学生分析解决问题的能力,当m取得最大值时,sinα最小,此时直线PM与抛物线相切,是解题的关键.

练习册系列答案
相关题目
已知命题p:函数y=sin4x是最小正周期为
的周期函数,命题q:函数y=tanx在(
,π)上单调递减,则下列命题为真命题的是( )
| π |
| 2 |
| π |
| 2 |
| A、p∧q |
| B、(¬p)∨q |
| C、(¬p)∧(¬q) |
| D、(¬p)∨(¬q) |
“a=1”是“函数f(x)=|x-a|+b(a,b∈R)在区间[1,+∞)上为增函数”的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |
过双曲线C:
-
=1的右顶点做x轴的垂线,与C的一条渐近线相交于点A,若以C的右焦点为圆心、半径为4的圆经过A,O两点(O为坐标原点),则双曲线C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|