题目内容
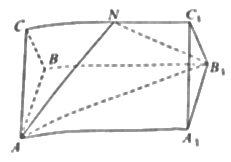
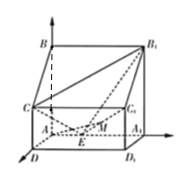
【题目】如图，四棱柱
中，
平面
，
，
，
，
，
为棱
的中点
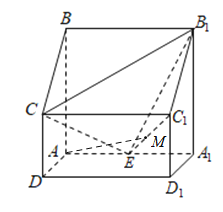
（1）证明：
；
（2）设点
在线段
上，且直线
与平面
所成角的正弦值为
，求线段的长.
【答案】（1）证明见解析；（2）
.
【解析】
（1）通过勾股定理计算证明证得
，再证得
，由此证得
平面
，从而证得
.
（2）建立空间直角坐标系，利用
得出
点的坐标，根据直线
与平面
所成角的正弦值为
列方程，解方程求得
的值，进而求得线段的长.
（1）在
中
，
，
，∴
，
∵
平面
，平面∥平面
，
∴平面，又
∥
，所以
平面，
所以且
∴平面，
∴
（2）由题可知，
，，
两两垂直，以
为原点，分别以
，，所在直线为
轴，
轴，
轴建立空间直角坐标系，
则
，
，
，
，
，
，
，设，则
则
易知
为平面的一个法向量.
设
为直线与平面所成角，则
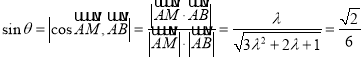
解得
，
（舍去）
所以
，
，故线段的长为.
练习册系列答案
相关题目
【题目】某校高三文科
名学生参加了
月份的高考模拟考试，学校为了了解高三文科学生的历史、地理学习情况，从名学生中抽取
名学生的成绩进行统计分析，抽出的名学生的地理、历史成绩如下表：
地理 历史 | [80,100] | [60,80） | [40,60） |
[80,100] | 8 | m | 9 |
[60,80） | 9 | n | 9 |
[40,60） | 8 | 15 | 7 |
若历史成绩在[80,100]区间的占30%，
（1）求
的值；
（2）请根据上面抽出的名学生地理、历史成绩，填写下面地理、历史成绩的频数分布表：
[80,100] | [60,80） | [40,60） | |
地理 | |||
历史 |
根据频数分布表中的数据估计历史和地理的平均成绩及方差（同一组数据用该组区间的中点值作代表），并估计哪个学科成绩更稳定.
