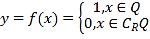题目内容
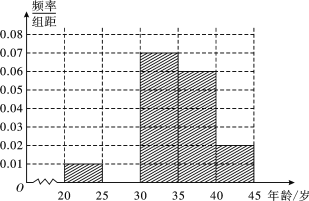
【题目】某车间4小时内生产了100根不同规格的三角钢材（单位：厘米），以
，
，
，
，
，
，
分组的频率分布直方图如图.
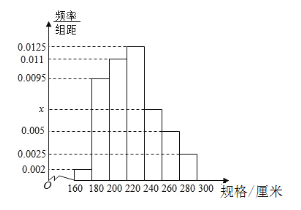
（1）求直方图中
的值；
（2）求这批钢材规格的众数；
（3）在规格为，，，的四组钢材中，用分层抽样的方法抽取11根钢材，则在的规格中应抽取多少根？
【答案】（1）
（2）230（3）5根
【解析】
（1）根据小矩形面积和为1，即可确定频率分布直方图中
的值；
（2）根据众数的意义，由最高小矩形底边的中点即可确定众数；
（3）先求得规格在
的钢材在四组钢材中所占比例，即可由抽取样本的总量求得在内应抽取的数量.
（1）依题意，
，
解得.
（2）由图可知，最高矩形的数据组为，
∴众数为
.
（3）规格在的钢材在四组钢材中所占比例为
，
∴规格在的钢材中应抽取
（根）.
浙江名校名师金卷系列答案【题目】为增强市民交通规范意识,我市面向全市征召劝导员志愿者,分布于各候车亭或十字路口处．现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示．
分组（单位：岁） | 频数 | 频率 |
| 5 |
|
| ① |
|
|
| ② |
|
|
|
|
|
|
合计 |
|
|
（1）频率分布表中的①、②位置应填什么数据？并在答题卡中补全频率分布直方图（如图）,再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数；
（2）在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加“规范摩的司机的交通意识”培训活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望．
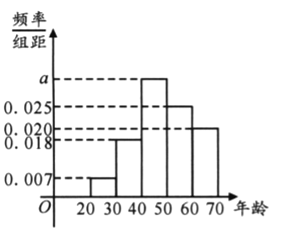
【题目】某保险公司给年龄在
岁的民众提供某种疾病的一年期医疗保险，现从
名参保人员中随机抽取
名作为样本进行分析，按年龄段
分成了五组，其频率分布直方图如下图所示；参保年龄与每人每年应交纳的保费如下表所示. 据统计，该公司每年为这一万名参保人员支出的各种费用为一百万元.
年龄 （单位：岁） |
|
|
|
|
|
保费 （单位：元） |
|
|
|
|
|
（1）用样本的频率分布估计总体分布，为使公司不亏本，求
精确到整数时的最小值
；
（2
之间的老人每
人中有
人患该项疾病(以此频率作为概率).该病的治疗费为
元，如果参保，保险公司补贴治疗费元.某老人年龄
岁，若购买该项保险(取
中的).针对此疾病所支付的费用为
元；若没有购买该项保险，针对此疾病所支付的费用为
元.试比较和的期望值大小，并判断该老人购买此项保险是否划算？
