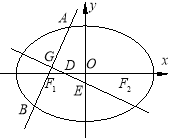题目内容
【题目】如图，四棱锥
中，底面
为矩形， 
面
， 
为
的中点。
（1）证明： 
平面
;
（2）设
， 
，三棱锥
的体积 
，求A到平面PBC的距离。
【答案】（1）证明见解析 （2） 
到平面
的距离为
【解析】试题分析：（1）连结BD、AC相交于O，连结OE，则PB∥OE，由此能证明PB∥平面ACE．（2）以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，利用向量法能求出A到平面PBD的距离
试题解析：(I）设BD交AC于点O，连结EO。
因为ABCD为矩形，所以O为BD的中点。
又E为PD的中点，所以EO∥PB
又EO
平面AEC，PB
平面AEC
所以PB∥平面AEC。
（II）
由
，可得
.
作
交
于
。
由题设易知
，所以
故
，
又
所以
到平面
的距离为
法2：等体积法
由，可得.
由题设易知,得BC
假设
的距离为d，
又因为PB=
所以
又因为
(或
)，
，
所以
阅读快车系列答案
【题目】为了解某校学生参加社区服务的情况，采用按性别分层抽样的方法进行调查．已知该校共有学生960人，其中男生560人，从全校学生中抽取了容量为n的样本，得到一周参加社区服务的时间的统计数据如下表：
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
（1）求m，n；
（2）能否有95多的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关？
（3）以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率，现从该校学生中随机调查6名学生，试估计6名学生中一周参加社区服务时间超过1小时的人数．
附：
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查，随机抽调了50人，他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
月收入(单位百元) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上统计数据填下面2×2列联表，并问是否有99％的把握认为“月收入以5500元为分界点对“楼市限购令”的态度有差异；
月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 | |
赞成 | a=______________ | c=______________ | ______________ |
不赞成 | b=______________ | d=______________ | ______________ |
合计 | ______________ | ______________ | ______________ |
(2)试求从年收入位于
（单位：百元）的区间段的被调查者中随机抽取2人，恰有1位是赞成者的概率。
参考公式：
，其中
.
参考值表：
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
