题目内容
已知函数f(x)=x2+mx+nlnx(x>0,实数m,n为常数).且n+3m2=0(m>0),若函数f(x)在x∈[1,+∞)上的最小值为0,则m=( )
A.e
| B.e
| C.
| D.-1 |
(1)当n+3m2=0时,f(x)=x2+mx-3m2lnx.
则f'(x)=2x+m-
=
=
令f'(x)=0,得x=-
(舍去),x=m.
①当m>1时,

∴当x=m时,fmin(x)=2m2-3m2lnm.
令2m2-3m2lnm=0,得m=e
.
②当0<m≤1时,f'(x)≥0在x∈[1,+∞)上恒成立,f(x)在x∈[1,+∞)上为增函数,当x=1时,fmin(x)=1+m.
令m+1=0,得m=-1(舍).
综上所述,所求m=e
.
故选:A.
则f'(x)=2x+m-
| 3m2 |
| x |
| 2x2+mx-3m2 |
| x |
| (x-m)(2x+3m) |
| x |
令f'(x)=0,得x=-
| 3m |
| 2 |
①当m>1时,

∴当x=m时,fmin(x)=2m2-3m2lnm.
令2m2-3m2lnm=0,得m=e
| 2 |
| 3 |
②当0<m≤1时,f'(x)≥0在x∈[1,+∞)上恒成立,f(x)在x∈[1,+∞)上为增函数,当x=1时,fmin(x)=1+m.
令m+1=0,得m=-1(舍).
综上所述,所求m=e
| 2 |
| 3 |
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
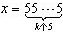 时,都有f(x)=
时,都有f(x)=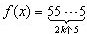 成立?请给出结论,并加以证明.
成立?请给出结论,并加以证明.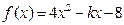 在
在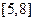 上是单调函数,则
上是单调函数,则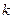 的取值范围是( )
的取值范围是( )