题目内容
已知函数f(x)=x2-2x,g(x)=ax+2,对任意的x1∈[-1,2],都存在x0∈[-1,2],使得g(x1)=f(x0),则实数a的取值范围是______.
当x0∈[-1,2]时,由f(x)=x2-2x得,
f(x0)=[-1,3],
又∵任意的x1∈[-1,2],都存在x0∈[-1,2],使得g(x1)=f(x0),
∴当x1∈[-1,2]时,g(x1)⊆[-1,3]
当a<0时,
,解得a≥-1;
当a=0时,g(x1)=2恒成立,满足要求;
当a>0时,
,解得a≤
综上所述实数a的取值范围是[-1,
]
故答案为:[-1,
]
f(x0)=[-1,3],
又∵任意的x1∈[-1,2],都存在x0∈[-1,2],使得g(x1)=f(x0),
∴当x1∈[-1,2]时,g(x1)⊆[-1,3]
当a<0时,
|
当a=0时,g(x1)=2恒成立,满足要求;
当a>0时,
|
| 1 |
| 2 |
综上所述实数a的取值范围是[-1,
| 1 |
| 2 |
故答案为:[-1,
| 1 |
| 2 |

练习册系列答案
相关题目
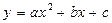 的图象如图所示,试判断
的图象如图所示,试判断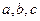 及
及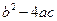 的符号。
的符号。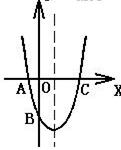
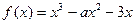 .
.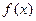 在
在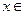 [1,+∞
[1,+∞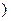 上是增函数,求实数
上是增函数,求实数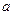 的取值范围;
的取值范围;