题目内容
已知二次函数f(x)=ax2+bx+c,(a≠0),且不等式f(x)<2x的解集为(-1,2).
(1)方程f(x)+3a=0有两个相等的实根,求f(x)的解析式.
(2)f(x)的最小值不大于-3a,求实数a的取值范围.
(3)a如何取值时,函数y=f(x)-(x2-ax+m)(|m|>1)存在零点,并求出零点.
(1)方程f(x)+3a=0有两个相等的实根,求f(x)的解析式.
(2)f(x)的最小值不大于-3a,求实数a的取值范围.
(3)a如何取值时,函数y=f(x)-(x2-ax+m)(|m|>1)存在零点,并求出零点.
∵f(x)<2x的解集为(-1,2).
∴ax2+(b-2)x+c<0的解集为(-1,2).…(1分)
∴a>0,且方程ax2+(b-2)x+c=0的两根为-1和2.
即
,所以
,
所以f(x)=ax2+(2-a)x-2a,(a>0)…(2分)
(1)∵方程f(x)+3a-0有两个相等的实根,即ax2+(2-a)x+a=0有两个相等的实根
∴△=(2-a)2-4a2=0,即3a2+4a-4=0,
∴a=-2或a=
…(3分)
∵a>0,∴a=
,∴f(x)=
x2+
x-
…(4分)
(2)f(x)=ax2+(2-a)x-2a=a(x+
)2+
∵a>0,∴f(x)的最小值为
,…(5分)
则
≤-3a,
即3a2+4a-4≤0,即-2≤a≤
,…(7分)
∵a>0,∴0<a≤
…(8分)
(3)由y=f(x)-(x2-ax+m)(|m|>1),得(a-1)x2+2x-(2a+m)=0(※)
①当a=1时,方程(※)有一解x=
+1,
函数=f(x)-(x2-ax+m)有一零点x=
+1,…(9分)
②当a≠1时,△=4[2a2+(m-2)a+(1-m)]
方程(※)有一解则△=4[2a2+(m-2)a+(1-m)]=0,令△1=4m2+4m-4≥0
得m≥2
-2或m≤-2
-2,∵|m|>1,即m>1或m<-1,
i)当m>1,a=
时,(a=
(负根舍去)),
函数y=f(x)-(x2-ax+m)有一零点x=
.…(10分)
ii)当m≤-2
-2时,a的两根都为正数∴当a=
或a=
时,函数y=f(x)-(x2-ax+m)有一零点x=
.(11分)
ⅲ)当-2
-2<m<-1时,△1=4m2+4m-4<0,∴△>0
③方程(※)有二解,所以△=4[2a2+(m-2)a+(1-m)]>0,
1)若m>1,△1=4m2+4m-4>0,a>
时,
(a=
(负根舍去)),函数y=f(x)-(x2-ax+m)
有两个零点x1,2=
=
;…(12分)
2)当m<-2
-2时,△1=4m2+4m-4>0,a的两根都为正数,
∴当a>
或0<a<
时,
函数y=f(x)-(x2-ax+m)有两个零点x1,2=
.…(13分)
ⅲ)当-2
-2≤m<-1时,△1=4m2+4m-4≤0,∴△>0恒成立,
∴a取大于0(a≠1)的任意数,函数y=f(x)-(x2-ax+m)有两个零点x1,2=
…(14分)
∴ax2+(b-2)x+c<0的解集为(-1,2).…(1分)
∴a>0,且方程ax2+(b-2)x+c=0的两根为-1和2.
即
|
|
所以f(x)=ax2+(2-a)x-2a,(a>0)…(2分)
(1)∵方程f(x)+3a-0有两个相等的实根,即ax2+(2-a)x+a=0有两个相等的实根
∴△=(2-a)2-4a2=0,即3a2+4a-4=0,
∴a=-2或a=
| 2 |
| 3 |
∵a>0,∴a=
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
(2)f(x)=ax2+(2-a)x-2a=a(x+
| 2-a |
| 2a |
| -8a2-(2-a)2 |
| 4a |
∵a>0,∴f(x)的最小值为
| -8a2-(2-a)2 |
| 4a |
则
| -8a2-(2-a)2 |
| 4a |
即3a2+4a-4≤0,即-2≤a≤
| 2 |
| 3 |
∵a>0,∴0<a≤
| 2 |
| 3 |
(3)由y=f(x)-(x2-ax+m)(|m|>1),得(a-1)x2+2x-(2a+m)=0(※)
①当a=1时,方程(※)有一解x=
| m |
| 2 |
函数=f(x)-(x2-ax+m)有一零点x=
| m |
| 2 |
②当a≠1时,△=4[2a2+(m-2)a+(1-m)]
方程(※)有一解则△=4[2a2+(m-2)a+(1-m)]=0,令△1=4m2+4m-4≥0
得m≥2
| 2 |
| 2 |
i)当m>1,a=
2-m+
| ||
| 4 |
2-m-
| ||
| 4 |
函数y=f(x)-(x2-ax+m)有一零点x=
| 1 |
| 1-a |
ii)当m≤-2
| 2 |
2-m+
| ||
| 4 |
2-m-
| ||
| 4 |
| 1 |
| 1-a |
ⅲ)当-2
| 2 |
③方程(※)有二解,所以△=4[2a2+(m-2)a+(1-m)]>0,
1)若m>1,△1=4m2+4m-4>0,a>
2-m+
| ||
| 4 |
(a=
2-m-
| ||
| 4 |
有两个零点x1,2=
-2±
| ||
| 2(a-1) |
-1±
| ||
| a-1 |
2)当m<-2
| 2 |
∴当a>
2-m+
| ||
| 4 |
2-m-
| ||
| 4 |
函数y=f(x)-(x2-ax+m)有两个零点x1,2=
-1±
| ||
| a-1 |
ⅲ)当-2
| 2 |
∴a取大于0(a≠1)的任意数,函数y=f(x)-(x2-ax+m)有两个零点x1,2=
-1±
| ||
| a-1 |

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
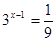 的解是
的解是 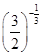 ×
×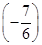 0+
0+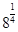 ×
×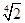 -
- =________.
=________.