题目内容
设f(x)=ax2+bx+c(a>b>c),f(1)=0,g(x)=ax+b.
(I)求证:函数f(x)与g(x)的图象有两个交点;
(Ⅱ)设函数f(x)与g(x)的图象的两个交点A、B在x轴上的射影为A1、B1,求|A1B1|的取值范围.
(I)求证:函数f(x)与g(x)的图象有两个交点;
(Ⅱ)设函数f(x)与g(x)的图象的两个交点A、B在x轴上的射影为A1、B1,求|A1B1|的取值范围.
(I)∵f(1)=0
∴a+b+c=0
∵a>b>c
∴a>0,c<0
由ax2+bx+c=ax+b得ax2+(b-a)x+c-b=0,
△=(b-a)2-4a(c-b)=(-a-c-a)2-4a(c+a+c)=c2-4ac
∵a>0,c<0
∴△>0所以函数f(x)与g(x)的图象有两个交点.
(II)由已知方程ax2+(b-a)x+c-b=0,两根为x1,x2,
x1+x2=
=2+
,x1x2=
=1+
,
|x1-x2|=
=
=
=
由a+b+c=0,a>b>c得a>0,c<0,a>-a-c>c,
于是得到,-2<
<-
,
∴|x1-x2|∈(
,2
)
所以,|A1B1|的取值范围(
,2
).
∴a+b+c=0
∵a>b>c
∴a>0,c<0
由ax2+bx+c=ax+b得ax2+(b-a)x+c-b=0,
△=(b-a)2-4a(c-b)=(-a-c-a)2-4a(c+a+c)=c2-4ac
∵a>0,c<0
∴△>0所以函数f(x)与g(x)的图象有两个交点.
(II)由已知方程ax2+(b-a)x+c-b=0,两根为x1,x2,
x1+x2=
| a-b |
| a |
| c |
| a |
| c-b |
| a |
| 2c |
| a |
|x1-x2|=
| (x1+x2)2-4x1x2 |
(2+
|
(
|
(
|
由a+b+c=0,a>b>c得a>0,c<0,a>-a-c>c,
于是得到,-2<
| c |
| a |
| 1 |
| 2 |
∴|x1-x2|∈(
| 3 |
| 2 |
| 3 |
所以,|A1B1|的取值范围(
| 3 |
| 2 |
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
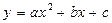 的图象如图所示,试判断
的图象如图所示,试判断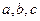 及
及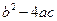 的符号。
的符号。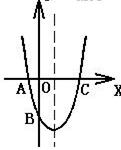
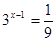 的解是
的解是