题目内容
附加题:是否存在一个二次函数f(x),使得对任意的正整数k,当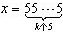 时,都有f(x)=
时,都有f(x)=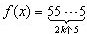 成立?请给出结论,并加以证明.
成立?请给出结论,并加以证明.
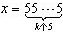 时,都有f(x)=
时,都有f(x)=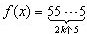 成立?请给出结论,并加以证明.
成立?请给出结论,并加以证明.存在符合条件的二次函数.
设f(x)=ax2+bx+c,则当k=1,2,3时有:
f(5)=25a+5b+c=55 ①; f(55)=3025a+55a+c=5555②; f(555)=308025a+555b+c=555555③.
联立①、②、③,解得a=
,b=2,c=0.
于是,f(x)=
x2+2x.
下面证明二次函数f(x)=
x2+2x符合条件.
因为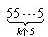 =5(1+10+100++10k-1)=
=5(1+10+100++10k-1)=
(10k-1),
同理: =
=
(102k-1);
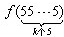 =f(
=f(
(10k-1))=
[
(10k-1)]2+2×
(10k-1)
=
(10k-1)2+2×
(10k-1)=
(10k-1)(10k+1)=
(102k-1)=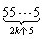
∴所求的二次函数 f(x)=
x2+2x符合条件.
设f(x)=ax2+bx+c,则当k=1,2,3时有:
f(5)=25a+5b+c=55 ①; f(55)=3025a+55a+c=5555②; f(555)=308025a+555b+c=555555③.
联立①、②、③,解得a=
| 9 |
| 5 |
于是,f(x)=
| 9 |
| 5 |
下面证明二次函数f(x)=
| 9 |
| 5 |
因为
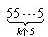 =5(1+10+100++10k-1)=
=5(1+10+100++10k-1)=| 5 |
| 9 |
同理:
 =
=| 5 |
| 9 |
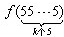 =f(
=f(| 5 |
| 9 |
| 9 |
| 5 |
| 5 |
| 9 |
| 5 |
| 9 |
=
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 9 |
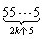
∴所求的二次函数 f(x)=
| 9 |
| 5 |

练习册系列答案
相关题目
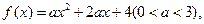 若
若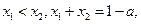 则 ( )
则 ( )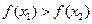
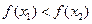
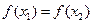
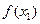 与
与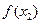 的大小不能确定
的大小不能确定