题目内容
【题目】已知函数![]() .
.
(1)研究函数![]() 的单调性;
的单调性;
(2)研究函数![]() 的零点个数情况,并指出对应
的零点个数情况,并指出对应![]() 的范围.
的范围.
【答案】(1)见解析;(2)当![]() 时,
时,![]() 存在唯一零点;当
存在唯一零点;当![]() 时,
时,![]() 无零点
无零点
【解析】
(1)首先确定函数定义域和导函数;分别在![]() 、
、![]() 、
、![]() 和
和![]() 四种情况下,根据导函数的正负,确定原函数的单调性;
四种情况下,根据导函数的正负,确定原函数的单调性;
(2)根据(1)中函数的单调性,分别在![]() 、
、![]() 、
、![]() 和
和![]() 四种情况下根据函数的极值和最值,结合单调性确定零点个数.
四种情况下根据函数的极值和最值,结合单调性确定零点个数.
(1)由题意得:![]() 定义域为
定义域为![]() ,
,![]()
①当![]() 时,令
时,令![]() 得:
得:![]()
则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
②当![]() 时,
时,![]() ,即
,即![]()
![]() 在
在![]() 上单调递增
上单调递增
③当![]() 时,
时,![]()
令![]() ,解得:
,解得:![]() ,
,![]()
![]()
![]()
则当![]() 和
和![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 在
在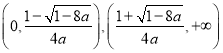 上单调递增,在
上单调递增,在 上单调递减
上单调递减
④当![]() 是,
是,![]()
令![]() ,解得:
,解得:![]() ,
,![]()
则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 在
在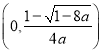 上单调递增,在
上单调递增,在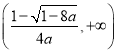 上单调递减
上单调递减
(2)①当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 不存在零点
不存在零点
②当![]() 时,
时,![]() 在
在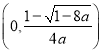 上单调递增,在
上单调递增,在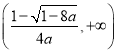 上单调递减
上单调递减
![]() 且
且![]()
![]()
![]() ,
,![]()
令![]() ,则
,则![]()
![]() 在
在![]() 上单调递增
上单调递增 ![]()
又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 不存在零点
不存在零点
③当![]() 时,
时,![]() 在
在![]() 上单调递增
上单调递增
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 必存在唯一零点
必存在唯一零点
④当![]() 时,
时,![]() 在
在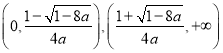 上单调递增,在
上单调递增,在 上单调递减
上单调递减
![]() 且
且![]()
![]() ,
,![]()
令![]() ,则
,则![]()
![]() 在
在![]() 上单调递增
上单调递增 ![]()
又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 必存在唯一零点
必存在唯一零点
综上所述:当![]() 时,
时,![]() 存在唯一零点;当
存在唯一零点;当![]() 时,
时,![]() 无零点
无零点

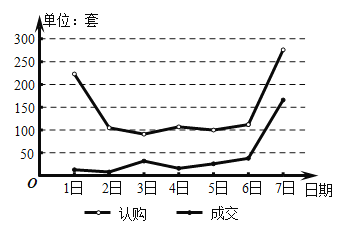
【题目】京剧是我国的国粹,是“国家级非物质文化遗产”,为纪念著名京剧表演艺术家,京剧艺术大师梅兰芳先生,某电视台《我爱京剧》的一期比赛中,2位“梅派”传人和4位京剧票友(资深业余爱好者)在幕后登台演唱同一曲目《贵妃醉酒》选段,假设6位演员的演唱水平相当,由现场40位大众评委和“梅派”传人的朋友猜测哪两位是真正的“梅派”传人.
(1)此栏目编导对本期的40位大众评委的年龄和对京剧知识的了解进行调查,根据调查得到的数据如下:
京剧票友 | 一般爱好者 | 合计 | |
50岁以上 | 15 | 10 | 25 |
50岁以下 | 3 | 12 | 15 |
合计 | 18 | 22 | 40 |
试问:在犯错误的概率不超过多少的前提下,可以认为年龄的大小与对京剧知识的了解有关系?
(2)若在一轮中演唱中,每猜出一位亮相一位,且规定猜出2位“梅派”传人”或猜出5人后就终止,记本轮竞猜一共竞猜![]() 次,求随机变量
次,求随机变量![]() 的分布列与期望.
的分布列与期望.
参考数据:
0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]()