题目内容
【题目】在平面直角坐标系
中，椭圆C：
（
）的左、右焦点分别为
，
，直线l：
交椭圆C于A，B两点，且
的周长为8.
（1）求椭圆C的方程；
（2）若线段
的中点为P，直线
与椭圆C交于M，N两点，且
，求直线l的方程.
【答案】（1）
（2）
【解析】
（1）先根据椭圆定义确定
的周长为
，再联立方程组解得
，即得结果；
（2）先根据椭圆几何性质化简
得
,再联立直线l的方程与椭圆方程，解得P点坐标，根据弦长公式以及韦达定理得
；根据P点坐标得
的直线方程，并与椭圆方程联立，根据弦长公式以及韦达定理得
；最后代入化简的关系式解得结果.
解：（1）因为直线l：
过椭圆C的左焦点
，所以
，
’
所以椭圆C：
（2）直线l的方程为
，与椭圆C联立得
，得
，所以
，
，
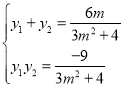所以
，
，
所以
过的直线方程为：
，联立
，得
而
，
因为
，
所以
，
所以
，所以
，
所以直线l的方程为
，即
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
