题目内容
15.在△ABC中,BC=2,∠A=45°,∠B为锐角,点O是△ABC外接圆的圆心,则$\overrightarrow{OA}$•$\overrightarrow{BC}$的取值范围是(-2,2$\sqrt{2}$].分析 首先建立恰当的直角坐标系,根据直角坐标系确定各点的坐标,进一步利用向量的数量积转化成利用定义域求三角函数的值域.最后求的结果
解答 解:如图所示: |BC|=2,∠BOC=90°,∠CAB=45°,
|BC|=2,∠BOC=90°,∠CAB=45°,
由于∠B为锐角,则:点A只能在左半圆上,
故设∠AOB=θ:A($\sqrt{2}$cosθ,$\sqrt{2}$sinθ)($\frac{π}{2}$$<θ<\frac{3π}{2}$)
B($\sqrt{2}$,0),C(0,$\sqrt{2}$)
所以:$\overrightarrow{OA}$=($\sqrt{2}$cosθ,$\sqrt{2}$sinθ),$\overrightarrow{BC}$=($-\sqrt{2},\sqrt{2}$)
$\overrightarrow{OA}•\overrightarrow{BC}$=-2cosθ+2sinθ=2$\sqrt{2}$sin($θ-\frac{π}{4}$),因为$\frac{π}{2}$$<θ<\frac{3π}{2}$,
所以$\frac{π}{4}<θ-\frac{π}{4}<\frac{5π}{4}$
则:-$\frac{\sqrt{2}}{2}$<sin($θ-\frac{π}{4}$)≤1,
所以-2<2$\sqrt{2}$sin($θ-\frac{π}{4}$)≤2$\sqrt{2}$,
故答案为:(-2,2$\sqrt{2}$].
点评 本题考查的知识要点:向量的数量积,三角函数的恒等变换,利用正弦型函数的定义域求值域.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.若$\overrightarrow{AB}$=3$\overrightarrow{a}$,$\overrightarrow{CD}$=-5$\overrightarrow{a}$,且|$\overrightarrow{AD}$|=|$\overrightarrow{BC}$|,则四边形ABCD是( )
| A. | 平行四边形 | B. | 菱形 | C. | 等腰梯形 | D. | 不等腰梯形 |
5.△ABC的外接圆的圆心为O,半径为1,若$\overrightarrow{AB}$+$\overrightarrow{AC}$=2$\overrightarrow{AO}$,且|$\overrightarrow{OA}$|=|$\overrightarrow{AC}$|,则△ABC的面积为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | 1 |
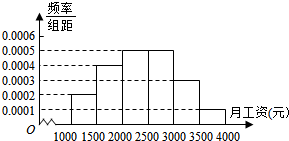 进入2014年金秋,新入职的大学生陆续拿到了第一份薪水.某地调查机构就月薪情况调查了1000名新入职大学生,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月薪在[1000,1500)单位:元).
进入2014年金秋,新入职的大学生陆续拿到了第一份薪水.某地调查机构就月薪情况调查了1000名新入职大学生,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月薪在[1000,1500)单位:元).